Tensors

Here is the first part of a series of courses of initiation to tensors.

What are tensors ? Beyond the definition of that notion, the study of tensors forms a theory with its own mathematical framework, namely a formal grammar expressing linear algebra better than by ordinary algebraic terms.

Why tensors ? The main motivation is its indispensability to express modern physics (General Relativity and
quantum physics) and even its usefulness to greatly clarify the expression of classical physics (conservation
laws in classical or relativistic mechanics, electromagnetism) which looks awful without it.

Unfortunately, usual courses of classical physics keep their old awkward formulations, missing the clarifications that tensors could provide, due to the bad reputation of tensors as a hard, inaccessible or messy topic to be reserved for a later year of teaching. Actually, this trouble relies on the way tensors are usually introduced, which I consider inappropriate, and could hopefully vanish by adopting a different approach. So, I will provide here my view on the topic in try to make it clearer and easier to learn.

I usually only make courses in text form, which is easier for me to work on. This would not suffice here because of geometrical aspects which need to be visualized. But I'm still more at ease writing than speaking. So I made here both text and video formats, which will be meant as complementary : some things will be only in video, others only in text.

1. Reminder on vector spaces and linear algebra.

A vector space is a set E with structures (operations)
satisfying the same identities as the operations with the same names in ℝ, when expressible between these sets.
From there, subtraction can be defined as

x − y = x + (-1).y

Vector spaces appear in geometry in different ways, where the 2 most intuitive are:
The latter is the most common way to imagine a vector space, which may involve new figures separate from those we could start with.

Vector spaces are classified by their dimension : a natural number, or infinity (the diversity of infinite dimensions does not matter for physics, we shall ignore it here).
ℝ is a 1-dimensional vector space.

For now, vector spaces (with dimension 2 or more) are handled without any measure of angles, or equivalently (in the sense of mutual definability) any distinction of squares among parallelograms, or of circles among ellipses. Vector spaces with such additional structures, called Euclidean vector spaces, will be discussed later.

We sometimes use complex vector spaces, replacing the role of the system ℝ of real numbers by that ℂ of complex numbers. So, ℂ is a 2-dimensional ℝ-vector space (precisely, an Euclidean one), but 1-dimensional as a complex vector space; n-dimensional complex spaces are 2n-dimensional in the sense of ℝ-vector spaces (not a priori Euclidean when n>1).

Important kind of vector space : the space EX of all functions from a set X to a vector space E. Its structures are defined from those of E.
Its dimension is : (Card X).(dim E)
So if E = ℝ, its dimension is Card X.

Vector subspace : subset stable by all operations (0,+,.)
Those of a 3D space E: {0}, straight lines and planes containing 0, and E.
The subspace of a vector space E generated by a set X ⊂ E is equivalently defined as
A vector space of functions from X to E : is a vector subspace of EX.

A function f : E → F between vector spaces E, F is linear (we shall say a linear map) if it preserves all operations.
Then its image (Im f) is a vector subspace of F, and its kernel
Ker f = {x∈E | f(x) = 0}
is a vector subspace of E.

For any vector space H of functions from X to E, any x∈X defines a linear map (f ↦ f(x)) from H to E.

The set L(E,F) of all linear maps from E to F is a vector space of functions (vector subspace of FE), thanks to the properties of operations. Its dimension is the product of dimensions (dim E).(dim F).

Linear maps from E to ℝ are called linear forms on E, or covectors.
The space E* of all covectors of E is called the dual of E.
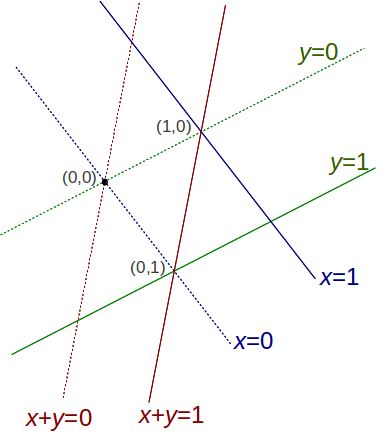
Nonzero covectors can be visualized by their kernel (hyperplane : dimension n−1) and its parallel space with value 1.
Sum of 2 linear forms

For any vector spaces E,F,G, an operation (function of 2 variables) : E×F → G is called bilinear if linear on each variable when the other is fixed, i.e. one curried form is in L(E, L(F,G)); equivalently the other curried form is in L(F, L(E,G)).

The operation ⚬ of composition of linear maps, from L(F,G)×L(E,F) to L(E,G), is bilinear. Naming elements as
f ∈ L(E,F)
g ∈ L(F,G)
g⚬f ∈ L(E,G)
the linearity on f (i.e of f ↦ g⚬f) is because g is linear.
The linearity on g still holds when only G is a vector space, and f is any function; there, it is deduced from the above (with H).

If E = ℝ then L(E,F) is essentially F (namely {(a ↦ a.x) | x∈F}), which gives the bilinearity of the function evaluator (g,y) ↦ g(y) from L(F,G)×F to G.

If G = ℝ we get the linearity of transposition from L(E,F) to L(F*,E*).

If F = ℝ we get the bilinearity of the tensor product
⊗ : G × E* → L(E,G)

This is just one of the possible definitions of the tensor product of elements, only equivalent for finite dimensional spaces.

But a proper understanding and formalization of tensors requires another definition of tensor products, allowing for any number of arguments, treated symmetrically. Here the symmetry of roles between G and E* can appear by transposing the target space, from L(E,G) to L(G*,E*).
But a symmetry between 2 definitions is not good. In their own framework, tensors will have 1 symmetric definition.

To make things really clean, we need to rebuild linear algebra on a different foundation: aside the usual definition and treatment of vector spaces which we shall call "algebraic", let us introduce another definition, as dual systems.

2. The category of dual systems

To provide the semantics for the tensorial formalism, linear algebra needs to be redefined from the concept of dual systems. This fact seems strangely unnoticed, as the big Wikipedia article on "dual systems" currently (2022) is not linked with articles on tensors either way, while the Wikipedia article on "dual spaces" only has small links with key phrases "dual systems" and "dual pairs", as if dual systems could only interest some analysis of infinite dimensional spaces. Also the article on dual systems assumes the background of all algebraic concepts on vector spaces, ignoring that linear algebra can be simplified by starting with dual systems to bypass some tedious aspects of the algebraic approach.

A dual system, or dual pair, is a pair of sets (E,E') qualified as "dual of each other", with an operation called duality pairing 
〈 , 〉 : E×E' → ℝ.
Only needed axioms:
Each curried form of a duality pairing is injective, with image a vector space of functions.
The injectivity of the curried form from E to E'* is written

∀x,y∈E, (∀z∈E', 〈x,z〉 = 〈y,z〉) ⇒ x = y.

We can write ⇔ instead of ⇒ since the converse always holds (an equality axiom).

Structures in each vector space E and E', are defined by copying those on their images, restrictions of those on spaces of all functions from given sets to ℝ, themselves defined from those of ℝ ; the axioms for algebraic vector spaces are deducible from identities in ℝ. This makes 〈 , 〉 bilinear.
We shall often identify E' with its copy as a subspace of E*, and also symmetrically, identify E with its copy as a subspace of E'* (letting the duality pairing play on both sides the role of function evaluator).

Both definitions (algebraic and with duality) are equivalent for finite dimension spaces (where the algebraic E* is the only possible dual of E) but not otherwise : for an infinite dimensional E, different infinite dimensional subspaces of E* may serve as duals of E.
Even, without the Axiom of Choice, there can exist vector spaces with no duality representative, that is when the natural map from E to E** is not injective. In particular the algebraic dual of an infinite dimensional space can have dimension 0. Such spaces have no interest for physics, so we shall ignore them.

Between dual pairs (E,E') and (F,F'), a map f : E→F will be qualified as transposable if

∀y∈F', ∃z∈E', ∀x∈E, 〈x,z〉 = 〈f(x),y〉

or in short
∀y∈F', y⚬f ∈E'
which means the existence of a (unique) function tf : F'→E' called the transpose of f, such that

∀x∈E, ∀y∈F', 〈f(x),y〉 = 〈x,tf(y)〉.

Seeing ℝ as part of the dual pair (ℝ,ℝ) with duality pairing given by multiplication, the condition for a y∈ℝE to be transposable from (E,E') to (ℝ,ℝ) is that y∈E' ; the transpose is then (a ↦ a.y).

Transposability implies linearity, and thus both properties are equivalent in finite dimensional cases.
In infinite dimensions, there is a concept of topological vector spaces, with continuous linear maps. For a certain topology, this condition of linearity+continuity coincides with transposability. Let us forget this and directly work with the simplest concept, that is the transposability of maps between dual systems.
Since the use of transposability will replace for us linearity, while the word "linearity" is much more familiar and equivalent to transposability for our main purpose (finite dimensional spaces), let us decide that from now on, we shall use the word "linearity" to actually mean transposability when used between spaces with given choices of duals. Similarly, the "bilinearity" of a binary operation will implicitly mean the transposability of the function it defines when either argument is fixed, if a dual is indeed given for the domain and target spaces of that function.

Dual pairs form a category, where morphisms from (E,E') to (F,F') are pairs of maps (f,f') where f : E→F and f': F'→E' are the transpose of each other.
In other words, f and f' play the roles of both curried forms of the same operation from E×F' to ℝ, where duality pairings play the role of function evaluator on both sides.
Compared to the usual function evaluator written y(x) for x∈E and y ∈ ℝE, the use of the pairing 〈x,y〉 requires that moreover, essentially, y belongs to the subspace E' of ℝE.

This operation E×F'∋(x,y) ↦ 〈f(x),y〉 is bilinear. Actually, the bilinearity of an operation from E×F' to ℝ is equivalent to the existence of such curried forms for it on both sides, thus transpose of each other and forming a morphism in this category.

Now the concept of tensor comes by considering that these 3 things :
being definable from each other, need to be seen as just 3 different roles of one same thing, called a tensor of order 2 with type (E', F), element of what we shall call the complete tensor product E'⊠F (which assumes the implicit data of the dual system which each space is seen a member of).

With conventions E'⊂ℝE and F'⊂ℝF, this definition for E'⊠F' (picking now F' instead of F) can also be written using the sum of functions ∐ as:

E'⊠F' = {∐f | f∈F'E} ⋂ {t∐g | g∈E'F}
= {h∈ℝE×F| (Im h⃗ ⊂ F') ∧ (Im h⃖ ⊂ E')}

3. Tensor notations

To work in practice with this concept of tensors of order n with their n+1 (or even more) different but equivalent uses as operations (which usual courses of linear algebra keep unfortunately distinguishing), we need to replace the notations we were using by a different notations system, that is the tensorial notations. Let us start with some definitions.

Generally, we shall call tensor any element of a vector space (which belongs to some dual system), and the type of a tensor is a way of naming this vector space it is seen an element of.
The order of a tensor, determined by its type, essentially means its arity, precisely the arity it takes as an operation with values in either ℝ or another 1-dimensional space (kind of quantity). Any tensor of order n, seen as an n-ary operation, must be n-linear (we shall say multilinear to not specify n), which means linear with respect to each of its arguments when others are fixed. So, the above tensor was said to be of order 2 because of its role as a bilinear operation with values in ℝ, but also because no further context was given for this construction. Actually the order attribute we give to vector spaces may depend on context.

All vector spaces which were given as primitive, and their duals, are said to be of order 1, except for ℝ and other 1-dimensional spaces, which are said to be of order 0 for reasons which will be clear later.
Just like operation symbols are symbols with n places for its arguments around, and families being synonyms for functions (unary operations) display their argument as an index, now a tensor of order n will be denoted as a symbol with places for n attached indices, which represent its arguments, although the arguments we may effectively give for it will not be written there.

Among the terms admitted in the tensor formalism, the monomial ones are those not using + or −, and therefore multilinear with respect to all occurrences of tensor symbols inside. The structure of these monomial terms will be expressed by the positions of index symbols attached to each tensor symbol, while the writing order between tensor symbols will be irrelevant.

So, given a dual pair (E,E'),

xi yi = xk yk = yi xi = 〈x,y〉

Repeated indices in a monomial are "internal to this monomial" and may be so renamed inside it without affecting its meaning.
Non-repeated indices matter as they represent the type of the value of this monomial as a tensor, and so must be repeated between monomials separated in the same equation by +, − , = ; they may only be globally renamed there.

The same tensorial formalism we are introducing, can be pictured by another notations system called the tensor diagram notation: monomial terms are figured as diagrams where

Actually in particle physics, Feynman diagrams need to be read as tensorial expressions in this way.

Now any tensor of order 2 (binary tensor) will be written with 2 indices. To take the same names as above, a binary tensor T ∈ E'⊠F, relating given dual pairs (E,E') and (F,F'), can be written Tij where
The axiom making them the transpose of each other is written

∀x∈E, ∀y∈F', (Tij xi) yj = xi (Tij yj)

This means that parenthesis are useless in monomials; they will be dropped there and only still used to contain both + and − operations, and also specify the scope of the differentiation symbol ∂.

Any dual pair (E,E') has a Kronecker delta symbol δ ∈ E'⊠E serving as the duality pairing of (E,E'), and equivalently as the identity function in each of E,E':

∀x∈E, δij xi = xj
∀y∈E', δij yj = yi
∀x∈E,∀y∈E', δij xi yj = xj yj = xi yi

Elements of 1-dimensional spaces, called quantities, are seen as of order 0 because they do not need an index in monomials, as they can be multiplied in any order, and tensors can be multiplied by them with the same rules in monomials as with real numbers. The only difference this makes from real numbers is the different 1-dimensional target space (instead of ℝ) of tensors and tensorial expressions as multilinear operations (it needs to be the same between monomials in an equation).

I had to introduce this definition and notation ⊠ for convenience, away from the tradition of only defining the tensor product ⊗ of vector spaces independently of their duals.
Another text will give the definition of the tensor product, with technical justifications for some aspects of the formalism we just developed, especially

4. Symmetry and antisymmetry

A tensor with all arguments in the same space is called

For a tensor T with order 2, it is symmetric if Tij =Tji, and antisymmetric if Tij = -Tji.
The spaces of symmetric tensors, and antisymmetric tensors, of order n in E (subspaces of ⊠n E = E ⊠ ... ⊠ E), are respectively denoted Symn E and Λn E.

As any involutive linear transformation is a reflection, the transposition of indices is a reflection in respect to the subspace of symmetric tensors, in parallel to that of antisymmetric ones.

Like any reflection, it can be used to express both linear projections, over each of these two subspaces in parallel to the other.
So, any tensor T ∈ E⊠E has a unique expression as a sum T = S + A where S is symmetric and A is antisymmetric, namely

Sij = (1/2).(Tij + Tji)
Aij = (1/2).(Tij − Tji)

The dimensions of both subspaces Sym2E and Λ2E can then be calculated as the traces of these projections to each (T ↦ S and T ↦ A), namely (with n = dim E)

dim Sym2E = n(n+1)/2
dim Λ2E = n(n−1)/2

Quadratic forms

Any tensor T ∈ E'⊠E' (bilinear form on E) defines a quadratic form Q = (E ∋ x ↦ T(x,x)). The kernel of this linear map (T↦Q) : E'⊠E' → ℝE is Λ2 E',
(why)
so that quadratic forms are actually presentations of symmetric tensors S ∈ Sym2 E.
Indeed we can restore S from Q as

∀x,y∈E, 2 S(x,y) = Q(x+y) − Q(x) − Q(y).

A more interesting formula uses the differential of Q as a field : the covector ∂jQ(x) is defined as ∂jQ(x) yj being an approximation of Q(x+y) − Q(x) for any small y. When y is small, Q(y) is neglected. So, the previous formula gives by approximation

∀x∈E, 2 Sij xi = ∂jQ(x)

The most often used symmetric bilinear forms are those whose quadratic form is positive on nonzero vectors : synonymously called "dot products" or "inner products" (in French there is only one name, "produit scalaire"). This is the fundamental structure giving an Euclidean geometry to a vector space. For this to describe the vectors of the usual physical space which has no most favorite unit of distance, its values are quantities (squared lengths).

The dot product in an Euclidean plane E (correspondence with its dual) can be understood by 3D drawings : either

Self-duality

If a tensor T ∈ E'⊠E' is invertible (also called "non-degenerate"), then T -1 ∈ E⊠E, and with the same property of symmetry or antisymmetry as T.
Giving such a T as a structure on E, can be formalized by declaring E to be self-dual, and using T as duality pairing. This is done only when T is either symmetric or antisymmetric (otherwise its symmetric and antisymmetric components would be 2 structures to distinguish on that space): a self-dual vector space is either qualified as
Unfortunately, this is usually done too often in usual teaching, so that people keep inappropriately defining as vectors what should rather be seen as covectors, to the point that they may have no clue what a covector is (unless they don't even know what a vector is either, as they only work with arrays of numbers serving as coordinates of anything, forgetting that, well, Nature does not fix a favorite choice of coordinates system in physical space). This can become a handicap as it binds them to Euclidean geometry and makes it harder for them to learn different geometries. And no, physical space is actually not Euclidean. 

Any 2-dimensional vector space is symplectic.
The dimension of a symplectic space is always even.
In a 2D Euclidean space (plane), composing its quadratic and symplectic structures gives its complex structure (multiplication by i).

5. Orthogonality

In a finite dimensional Euclidean vector space E, 2 vectors x,y are said to be orthogonal if 〈x,y〉 = 0.
This defines a Galois connection, which is symmetric : (⊥,⊥) ∈ Gal(℘(E), ℘(E)).
The closed elements of this connection are the vector subspaces.
The closure of a set is the vector subspace it generates.
If E has dimension n and a subspace F ⊂ E has dimension k then ⊥F has dimension n−k because a basis of F and a basis of ⊥F together form a basis of E.

Now these definitions do not really need the space to be Euclidean, except for the argument with basis, which needs to be replaced.

For any dual pair (E,E'), orthogonality defines in the same way a Galois connection (⊥,⊤) ∈ Gal(℘(E),℘(E')).
Again on each side, closed elements are the vector subspaces.
Except that, infinite dimensional subspaces are not always closed. So, the study of infinite dimensional dual pairs requires to speak about closed subspaces, which are a special kind of vector subspace. We shall not really care about this, but will still write general definitions in ways still valid then.
Now, in the usual visualization of an n-dimensional vector space E as a set of points, a k-dimensional subspace H of E' can be visualized by means of its orthogonal, that is an (n−k)-dimensional subspace F of E.
Namely H can be seen as a dual of the quotient space E/F.
Drawing of quotient in https://spoirier.lautre.net/no12.pdf page 8.

In any dual pair (E,E'), any subspace F ⊂ E naturally gets a dual F' = tIdF [E'] making IdF an embedding from (F,F') to (E,E').
Here, Ker tIdF = ⊥F.
Then (tIdF is a quotient from (E',E) to (F',F)) ⇔ (F is closed).

Any binary tensor T = (f, f') ∈ E⊠F where f : E'→F and f': F'→E has a left image Im f' ⊂ E and a right image Im f ⊂ F.

It also has a left kernel Ker f = ⊥Im f' ⊂ E' and a right kernel Ker f'= ⊥Im f ⊂ F', which are closed subspaces.

As well-known in linear algebra, the equivalence relation ∼f of any linear map f is expressible from Ker f as

x ∼f y ⇔ x − y ∈ Ker f

Generally, from any subspace A ⊂ E, we can define an equivalence relation this way (x ∼ y ⇔ x − y ∈ A), making the quotient E/A a vector space.
However, for this quotient to be part of a dual system making transposable the surjection ϕ: E ↠ E/A we need A to be closed. Then its transpose is injective, ϕ' : (E/A)' ↪ ⊥A and ⊥A is the closure of Im ϕ'. Now to make ϕ a quotient we must take ⊥A as dual of E/A, letting this construction coincide with the above one for the embedding of ⊥A into E'.
There is only the inessential difference that we now define the quotient as proceeding by an equivalence relation, while it was previously defined by restricting covectors, seen as functions, on a subspace. To make things explicit, the duality pairing on (E/A, ⊥A) can be defined by

∀x∈E,∀x∈⊥A, 〈ϕ(x),y〉 = 〈x,y〉.

Similarly, any binary tensor T = (f, f') ∈ E⊠F defines a pairing between its left image Im f' ↔ F'/Ker f' and its right image Im f ↔ E'/Ker f . Thus, these 4 spaces have the same dimension, which is called the rank of T.

Antisymmetrization

The p-antisymmetrizer, officially called the generalized Kronecker delta of order 2p over a given dual pair (E,E'), has p upper indices and p lower indices. It "provides antisymmetry" over p indices, may they be all up or all down, by summing up all diagrams expressing the p! permutations of these indices, with sign given by the signatures of these permutations. Thus, it maps any tensor of order p to its antisymmetric component multiplied by p!.
For example with p = 2,

δijkl = δik δjl − δil δjk

Given a dual pair (E,E') with dimension n, the space Λn E' is 1-dimensional, represented by a generating element εijk... we shall call a/the lower Levi-Civita symbol of E. This tensor gives the determinant of any n-tuple of vectors in E, i.e. the volume of the parallelepiped they form, with sign expressing their orientation.
(Why : drawings 2D, 3D..)
It can be seen as an antisymmetric n-linear map from En to a copy of Λn E seen as a separate 1-dimensional space, namely the vector line of quantities "volumes in E signed by the orientation". The space E is said to be oriented if qualifications of "positive" vs "negative" are given to both sides of this line. Any choice of lower Levi-Civita symbol of E, namely a choice of a favorite or no favorite unit of volume, and a choice of orientation or no orientation, determines the convention for its "inverse" : the upper Levi-Civita εijk... symbol of E, generator of Λn E, playing a symmetric role by duality. Namely, when seen as an n-linear form on E', it takes value in a copy of Λn E always considered as "the inverse line" to Λn E'.

Namely, this inversion rule, to define "the same unit of volume" and "the same orientation", is such that their product gives the antisymmetrizer: for example

εij εkl = δijkl

Representing subspaces by antisymmetric tensors


Any k-dimensional subspace A ⊂ E, can be given in the form of its upper Levi-Civita symbol, i.e. a generator of Λk A ⊂ Λk E. It can be obtained by applying the antisymmetrizer to a basis of k elements of A (which gives it the volume of this basis). For example with k=2, and a basis (a,b) of A, this is written a∧b. In index notations,

(a∧b)kl= δijkl ai bj = ak bl − al bk

Now the (n−k)-dimensional subspace ⊥A of E' where n = dim E, is similarly expressible by its Levi-Civita symbol, generator of Λn−k ⊥A ⊂ Λn−k E', which can also be written from a basis of A using the lower Levi-Civita symbol of E. Namely with k=2 and n=5, and a basis (a,b) of A,
εijklm ai bj

6. Review of quadratic spaces

In the same way, other kinds of bilinear forms give other geometries. Unfortunately, usual courses do not have a name for these other structures, as if they were not real, though our actual physical space is not Euclidean. Because it is 4D, described by the Minkowski geometry, which differs from Euclidean geometry by the fact the scalar square of its vectors is not positive. According to Wikipedia, where it is described, "The Minkowski inner product is not an inner product", and "It is also called the relativistic dot product".

Quadratic forms 2D are represented by paraboloids.
(google images)
 Wikipedia : Paraboloid : image of elliptic paraboloid, parabolic cylinder, hyperbolic paraboloid

Quadratic forms 3D appear by "their spheres" which are quadrics
 Illustrations(12.6.13).
Geometric description of orthogonality of subspaces with respect to a cone.

For any quadratic form (with bilinear form b), its signature is a pair (p,q) where

Then the rank of b is p+q. Thus p+q = n if b is non-degenerate in an n-dimensional space.
Essentially, signatures (p,q) and (q,p) are synonymous, describing the same geometry, since they are exchanged when replacing b by -b.

A subspace A ⊂ E of a quadratic space, is called regular if A ∩ ⊥A = {0}. Equivalently, the restriction to A of the inner product of E is non-degenerate, making A a quadratic space.

The symplectic structure of a 2-dim space E gives an isomorphism between E and E', thus between E⊠E and E'⊠E', and between Sym2 E and its dual Sym2 E'. This makes Sym2 E a quadratic space with signature (1,2).
Illustration.

Correspondence between directions in E and directions in the cone (symmetric squares of vectors).
The null directions of a quadratic form (b ∈ Sym2 E) in E are those of the intersection of ⊥b with the cone.
Illustration of the symmetric product of 2 vectors : orthogonal to both vectors

...

The symplectic structures of two 2-dim spaces E, F give an isomorphism between E⊠F and E'⊠F'. This makes E⊠F a quadratic space with signature (2,2).
Its null vectors are the rank 1 tensors.
Illustration by using the previous representation (E = F), 3D + the 4th dimension representing the antisymmetric part.

Illustration in projective form : the cone appears, depending on the choice of projective representation, either as an hyperbolic paraboloid, or as a hyperboloid. In each case, we notice a grid of straight lines, which correspond to the x⊗y for fixed x and variable y, or vice versa. The view as an hyperboloid corresponds to the view (E = F) as the subspace of symmetric tensors is sent to infinity.

Finally, starting with a 4D space E, its Levi-Civita symbol gives to the space Λ2E (antisymmetric binary tensors) a quadratic structure (let us write it ε) with signature (3,3). Its cone is made of (antisymmetric) elements with rank 2, while other elements have rank 4; it contains 2 kinds of 3D vector subspaces (which correspond to the duality of roles of E and E'):

If E is also given a quadratic structure then this brings another quadratic structure b on Λ2E with signatures as follows

Signature of E Signature of b
(4,0) or (0,4)
 (6,0)
(3,1) or (3,1)
 (3,3)
(2,2)
 (2,4)

Composing ε and b gives a transformation of Λ2E. In the cases of even signatures ((4,0) or (2,2)) this transformation is a reflection (involution), splitting Λ2E as a sum X+Y of two quadratic 3D subspaces.
In the (2,2) case the restrictions of b to X and Y have signature (1,2) and represent Sym2 A and Sym2 B where E= A⊠B.

In the (4,0) case, X and Y are of course Euclidean. This role of a 4D Euclidean space as a space of correspondences between two 3D Euclidean spaces, appears in particular to represent the structure of the set of all maximally entangled states of a system of 2 qbits; it also has strong links with the algebra of quaternions.
Giving an element i of X then amounts to giving to E a complex structure (then a Hilbert space with 2 complex dimensions), whose 1D complex projective space corresponds to the sphere of Y. Then completing i to form an orthogonal basis (i,j,k) of X, these j,k form the real and imaginary parts of a Levi-Civita symbol for E as a 2D complex space.

In a Minkowski space E (signature (3,1)) this composition of ε and b gives not a reflection but a complex structure, making Λ2E a complex quadratic space, with complex dimension 3, and its complex bilinear symmetric form is b + i ε where each of b and ε is meant in its initial sense of real bilinear form. An important role of Λ2E is as the space of values of the electromagnetic field at a point of space-time. A choice of reference frame (time direction) leads to a split of its elements as E + i B where E and B are the "electric" and "magnetic" fields in 3D.
This 3D quadratic complex space, similarly to real quadratic spaces with signature (1,2), can be seen as the space of symmetric bilinear forms on a 2D complex space called the space of spinors of space-time. Its 1D complex projective space, transformed by the Möbius transformations, represents the sphere of vision (set of directions in the light cone), while E plays the role of its space of Hermitian forms.

7. Screw theory

Infinitesimal rotations

Let E a vector space, g ∈ E⊠E and ω∈ E'⊠E'. Interpret g⚬ω as a speeds field, i.e. representing infinitesimal transformations on E written rij = δij + ωik gkj close to δij.
The condition for r to preserve g (i.e. rij rkl gik = gjl) is then

ωik gkj gil + ωik gkl gji = 0jl

Renaming indices,
(ωki gij + ωik gji) gkl = 0jl
If g is invertible (which makes {g⚬ω | ω∈ E'⊠E'} the set of all infinitesimal transformations of E), this is simplifiable as
ωki gij + ωik gji = 0kj. Therefore,
Assume g is symmetric. We just showed that the space of infinitesimal rotations in a quadratic vector space E is identifiable with Λ2E'.
Now for the concerns of physics, we need to describe the infinitesimal rotations of a quadratic affine space (such as an Euclidean affine space or a Minkowski space-time, which are the relevant kinds of spaces for physics).
For this, an n-dimensional affine space A will be formalized as A= {x ∈ E|〈x,u〉=1} in an (n+1)-dimensional vector space E with a fixed covector u. Then the n-dimensional vector space V = Ker u plays the role of the "space of vectors" (translations) of A.
Now a quadratic structure on A, is formalized by a metric g ∈ Sym2 V ⊂ Sym2E with rank n.
Then the space of infinitesimal rotations of A is also isomorphic to Λ2E', expressible as {g⚬ω |ω∈ Λ2E'}. Indeed:

Wrenches

Consider an elastic object O attached in equilibrium with potential energy U between two rigid sides K and K', with no other external forces involved. Then U varies when small rotations are applied to each of K and K'. We define the wrench exerted by K on O as the differential of U with respect to rotations of K while K' stays fixed. Such variations of energy in O are "provided by" K as it slowly moves, through its link with O.

The sum of both wrenches exerted by K and K' on O cancels. This is because when K and K' follow the same rotation, the whole of O will naturally also follow that rotation, staying in its state of equilibrium with constant energy.

Let us say that the wrench is spatially conserved as it flows from K to O and then from O to K'.
The vector space of wrenches is the dual of that of infinitesimal rotations, which we described as Λ2E'.
Thus, it can be identified as Λ2E.
In particular, the wrench of a force F∈V exerted at a point P∈A is P∧F∈ Λ2E.
Any wrench ω∈Λ2E contains the data of the force F=ω(u), i.e. Fj = ωij ui while the rest of its data is usually referred to as the torque with respect to any chosen origin of space.

The reason why both spaces of infinitesimal rotations and wrenches are usually confused as a single mathematical concept of "screw", though they are basically dual and distinct, comes from a coincidence due to the 3-dimensionality of the affine Euclidean space in which they are usually introduced: as the space E then used has dimension 4, its Levi-Civita symbol gives an isomorphism between Λ2E and Λ2E' (which is actually of no use).

There is of course no such isomorphism when applying these constructions to the 4D Minkowski space-time, which is the actual space involved in theoretical physics.
Indeed, the same concepts hold there, once replaced the name "potential energy" by "action". Then the names of the components "force" and "torque" of a wrench, respectively become "Four-momentum" (split as the data of "energy" and "momentum" in a given reference frame), and "Relativistic angular momentum" (split as the data of the angular momentum, and the "mass moment" giving the position of the center of mass). I do not know a name for the whole equivalent of "wrench" there.

The stress-energy tensor

Introduction to General Relativity


Tensor product : technical complement to justify the tensor formalism.