1.3. Form of theories: notions, objects and meta-objects
The variability of the model
Each theory describes its model as a fixed system. But from
the larger viewpoint of model theory, this is a mere «choice» of one possible model
(interpretation) in a (usually infinite) range of other existing, equally legitimate models of
the same theory. Now this fixation of the model, like the fixation of any variable, is just the
simple act of picking any possibility, ignoring any issue of how to specify an example in
this range. Actually these «choice» and «existence» of models can be quite abstract. In
details, the proof of the Completeness
theorem will effectively «specify» a model of any consistent theory for the general case,
but this definition will not be very explicit, due to its use of infinity. Regardless this difficulty,
the attitude of implicitly fixing a model when formally studying any mathematical theory,
remains the normal way of interpreting it (except somehow for set theory as explained in 2.A).
Notions and objects
Each theory has its own list of notions (usually designated
by common names), formally serving as the kinds of variables it can use
; each model interprets each notion as a set that is the common
range of all variables of this kind. For example, Euclidean geometry
has the notions of «point», «straight line», «circle» and more, and is usually
expressed using a different style of variable symbol for each. The
objects of a theory in a model, are all possible values
of its variables of all kinds (the elements of all its notions) in this model.
One-model theory
Any discussion on several theories T and systems M that may be
models of those T, takes place in model theory, with its
notions of «theory» and «system» that are the respective kinds of the variables
T and M. But when focusing on one theory with a fixed model, the
variables T and M now fixed disappear from the list of variables.
Their kinds, the notions of theory and model, disappear from the notions list too.
This reduces the framework, from some model theory, to that of a one-model theory.
A model of a one-model theory, is a system [T,M] which combines
a theory T with a model M of T.
The diversity of logical frameworks
The role of a logical
framework, as a precise version of (one-)model theory with its
proof theory, is to describe :- The admissible forms of contents for theories ;
- In particular, the syntactic structures of possible statements and other
expressions, which can be called their "grammar" ;
- The meaning of these contents and expressions on the models ;
- The rules of development of theories.
Here are those we shall see,
roughly ordered from the poorest to the most expressive
(though the order depends on the ways to relate them):
- Boolean algebra, also called propositional calculus (1.6);
- Algebra;
- First-order logic;
- Duality (for geometry) and the tensor formalism for linear algebra;
- Second-order logic (5.1, 5.2);
- Higher-order logic (5.2);
- Strong versions of set theory (1.A).
We shall first describe the main two of them in parallel. First-order logic is the
most common version of model theory, describing first-order theories we shall
also call generic theories. Set theory, which can encompass all
other theories, can also encompass logical frameworks and thus serve itself as
the ultimate logical framework as will be explained in 1.D.
Most frameworks manage notions as types (usually in finite number for
each theory) classifying both variables and objects. Notions are called types if
each object belongs to only one of them, which is then also called the type of
the variables that can name it. For example, an object of Euclidean
geometry may be either a point or a straight line, but the same
object cannot be both a point and a straight line. But set theory will need
more notions beyond types: classes, which will be introduced in 1.7.
Examples of notions from various theories
| Theory |
Kinds of objects (notions) |
| Generic theories |
Urelements classified by types to play different roles |
| Set theory |
Elements, sets, functions, operations,
relations, tuples... |
| Model theory |
Theories, systems and their components
(listed below) |
| One-model theory
|
Objects, symbols, types or other notions, Booleans,
structures (operators, predicates), expressions (terms, formulas)... |
| Arithmetic |
Natural numbers |
| Linear Algebra |
Vectors, scalars... |
| Geometry |
Points, straight lines, circles... |
Meta-objects
The notions of a one-model theory (1MT), normally interpreted in [T,M], classify
the components of T («type», «symbol», «formula»...), and those of M («object»,
and tools to interpret components and expressions of T there).
But the same notions (which may belong to another logical framework) can be interpreted in
[1MT, [T,M]], by putting the prefix meta- on them.
By its notion of «object», each one-model theory distinguishes the
objects of T in M from the rest of its own objects in [T,M],
which are the meta-objects. The above rule of use of the meta prefix
would let every object be a meta-object; but we will make a vocabulary
exception by only calling meta-object those which are not objects:
symbols, types or other notions, Booleans, structures, expressions...
Set theory only knows the ranges of some of its own variables, seen
as objects (sets). But, seen by one-model theory, every variable of
a theory has a range among notions, which are meta-objects only.
Components of theories
In a given logical framework, the content of a theory consists in 3
lists of components of the following kinds, where those of each of the latter
two kinds are finite systems using those of the previous kind.
- A list of abstract types, names that will designate the types in each system;
- A language (vocabulary): list of structure
symbols, names of the structures which will form the described system (1.4).
- A list of axioms chosen among expressible statements with
this language (1.9).
Set-theoretical interpretations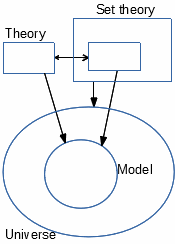
Any generic theory can be interpreted (inserted, translated) in set theory
by converting its components into components of set theory. This is the usual
view of ordinary mathematics, seeing many systems as «sets with relations or
operations such that...», with possible connections between these systems.
Let us introduce both the generic interpretations applicable to any generic
theory, and other ones usually preferred for some specific theories.
Any interpretation converts each abstract type into a symbol (name) designating
a set called interpreted type (serving as the range of variables of that type,
whose use is otherwise left intact). This symbol is usually a fixed variable in the
generic case, but can be accepted as constant symbol of set theory in special
cases such as numbers systems (ℕ, ℝ...).
In generic interpretations, all objects (elements of interpreted types) are
urelements, but other kinds of interpretations called standard
by convention for specific theories may do otherwise.
For example, standard interpretations of geometry represent points by
urelements, but represent straight lines by sets of points.
Generic interpretations will also convert structure symbols into fixed variables
(while standard ones may define them using the language of set theory).
Any choice of fixed values of all types and structure symbols, defines a choice of
system. When the language is seen
as a set (in particular if it is finite) which is usually the case, models are themselves
objects of set theory, owing
their multiplicity to the variability of types and structure symbols. This integrates
all needed theories into the same set theory, while gathering representatives
of all their considered models inside a common model of set theory. This is
why models of set theory are called universes. When adopting set
theory as our conceptual framework, this concept of "interpretation" becomes
synonymous with the choice (designation) of a model.
Other languages:
FR : 1.3. Forme des
théories: notions, objets, méta-objets