1.3. Forme des théories: notions, objets et méta-objets
La variabilité du modèle
Chaque théorie
décrit son modèle comme un système fixe. Mais du point de vue plus large de la
théorie des modèles, cela n'est qu'un simple «choix» d'un modèle (interprétation)
possible dans une diversité (généralement infinie) d'autres modèles
existants, également légitimes, de la même théorie. Or, cette fixation du modèle,
comme la fixation de toute variable, n’est que le simple acte de choisir une
possibilité, en ignorant toute question de savoir comment spécifier un exemple.
En fait, ces «choix» et «existence» de modèles peuvent être très abstraits. En
détail, la preuve du théorème de complétude «spécifiera» effectivement un
modèle de toute théorie cohérente pour le cas général, mais cette définition
ne sera pas très explicite, par son usage de l'infini.
Sans égard à cette difficulté, l’attitude de fixer implicitement un modèle lorsqu’on
étudie formellement une théorie mathématique, reste la manière normale de l'interpréter
(sauf en un sens pour la théorie des ensembles comme expliqué en 2.A).
Notions et objets
Chaque théorie a sa propre liste de notions (couramment désignées
par des noms communs), qui lui servent formellement de sortes de variables
utilisables. Chaque modèle interprète chaque notion comme un ensemble qui
est le domaine commun de toutes les variables de cette sorte. Par exemple,
la géométrie euclidienne a les notions de «point», «ligne droite»,
«cercle» et plus, et est habituellement exprimée en utilisant un style différent
de symboles de variables pour chacune. Les objets d'une théorie dans un
modèle, sont toutes les valeurs possibles de ses variables de toutes
sortes (éléments de toutes ses notions) dans ce modèle.
Théorie du modèle
Toute discussion sur plusieurs théories T et systèmes M modèles possibles de
ces T, s'effectue dans la théorie des modèles, avec ses notions de «théorie»
et «système» qui sont les sortes respectives des variables T et M.
Mais en se concentrant sur une théorie avec un modèle fixe, les
variables T et M étant fixées disparaissent de la liste
des variables. Leurs sortes, les notions de théorie et de modèle,
disparaissent ainsi de la liste des notions. Ceci réduit le cadre, d'une
théorie des modèles à une théorie du modèle.
Un modèle d'une théorie du modèle, est un système [T,M]
combinant une théorie T et un modèle M de T.
Sur la diversité des cadres logiques
Le rôle d'un cadre
logique, version précise de la théorie du modèle ou des
modèles avec sa théorie des preuves, est de décrire
- Les formes admissibles de contenus des théories ;
- En particulier, les structures syntactiques des énoncés possibles
et d'autres expressions, que l'on peut appeler leur "grammaire";
- La signification de ces contenus et expressions sur les modèles
- Les règles de développement des théories
Voici ceux que nous présenterons, grossièrement ordonnés du plus pauvre
au plus expressif (bien que l'ordre dépende des manières de les relier):
- L'algèbre booléenne, aussi appelée calcul propositionnel (1.6);
- Algèbre;
- Logique du premier ordre
- La dualité (pour la géométrie) et le formalisme tensoriel pour l'algèbre linéaire;
- Logique du second ordre (5.1, 5.2);
- La logique d'ordre supérieur (5.2);
- Des versions fortes de la théorie des ensembles (1.A).
Nous allons d'abord décrire les deux principaux cadres logiques en parallèle.
La logique du premier ordre est la version la plus courante de la théorie des modèles,
décrivant les théories du premier ordre que nous appellerons également
théories génériques. La théorie des ensembles, qui peut englober
toutes les autres théories, pourra également englober les cadres logiques et
ainsi servir elle-même de cadre logique ultime, comme sera expliqué en
1.D.
Le qualificatif "ensembliste" visera à qualifier tout concept appartenant à,
ou se rapportant à, la théorie des ensembles.
La plupart des cadres gèrent les notions comme des types
(habituellement en nombre fini pour chaque théorie), classifiant à la fois
variables et objets. Les notions sont appelées des types si chaque objet
n'appartient qu'à un seul d'entre eux, qu'on appelle alors aussi le type des
variables qui peuvent le désigner. Par exemple, un objet de la géométrie
euclidienne peut être un point ou une droite, mais le même objet ne peut
être à la fois un point et une droite. Mais la théorie des ensembles aura besoin
d'autres notions que les types: les classes, qui seront introduites en 1.7.
Exemples de notions de diverses théories
| Théorie |
Sortes d'objets (notions) |
| Théorie générique |
Urelements classés par types pour jouer divers roles |
| Théorie des ensembles |
Eléments, ensembles, fonctions, opérations,
relations, uplets... |
| Théorie des modèles |
Théories, systèmes et leurs
composants (détaillés ci-dessous). |
| Théorie du modèle |
Objets, symboles, types ou autres notions, Booléens,
structures
(opérateurs, prédicats), expressions (termes, formules)... |
| Arithmétique |
Nombres entiers |
| Algèbre linéaire |
Vecteurs, scalaires... |
| Géométrie |
Points, droites, cercles... |
Méta-objets
Les notions d'une théorie du modèle (1MT), normalement interprétées dans [T,M],
classifient les composants de T («type», «symbole», «formule»...) et ceux de
M («objet», et des outils pour y interpréter les composants et expressions
de T). Mais les mêmes notions (pouvant appartenir à un autre cadre logique)
pourront être interprétées dans [1MT, [T,M]], en les marquant du préfixe méta-.
Par sa notion d'«objet», chaque théorie du modèle distingue les objets de T dans M,
du reste de ses propres objets dans [T,M] qui sont les méta-objets. La règle
ci-dessus d'utilisation du préfixe méta admettrait tout objet comme un méta-objet ;
mais on fera une exception de vocabulaire en réservant le nom de
méta-objet à ceux qui ne sont pas des objets : symboles,
types ou autres notions, Booléens, structures, expressions...
La théorie des ensembles ne connait que les domaines de certaines de
ses variables, vus comme objets (ensembles). Mais, vue par la théorie
du modèle, toute variable d'une théorie a un domaine parmi les
notions, qui ne sont que des méta-objets.
Composants des théories
Dans un cadre logique donné, le contenu d'une théorie consiste en 3 listes
de composants de sortes suivantes, où ceux de chacune des 2 dernières
sortes sont des systèmes finis utilisant ceux de la sorte précédente:
- Une liste de types abstraits, noms qui désigneront les types dans chaque système;
- Un langage (vocabulaire) : liste de symboles de
structure, noms des structures qui formeront le système décrit (1.4).
- Une liste d'axiomes choisis parmi les énoncés exprimables
avec ce langage (1.5).
Interprétation ensembliste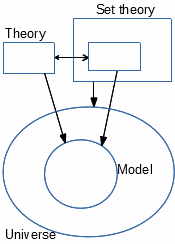
Toute théorie générique peut être interprétée (insérée, traduite) en théorie des
ensembles, en convertissant ses composants en composants de la théorie des
ensembles. C'est l'approche habituelle des mathématiques ordinaires, voyant de
nombreux systèmes comme «ensembles avec des relations ou des opérations
telles que ...», avec des connexions possibles entre ces systèmes. Introduisons
à la fois les interprétations génériques applicables à toute théorie
générique, et d'autres habituellement préférées pour certaines théories spécifiques.
Toute interprétation convertit chaque type abstrait en un symbole (nom)
désignant un ensemble appelé type interprété (servant de domaine aux
variables de ce type, dont l'usage reste par ailleurs intact). Ce symbole est
habituellement une variable fixe dans le cas générique, mais peut être accepté
comme symbole de constante de la théorie des ensembles dans des cas
spéciaux comme les systèmes de nombres (ℕ, ℝ...).
Dans les interprétations génériques, tous les objets (éléments des types interprétés)
sont des urelements, mais d'autres sortes d'interprétations dites standard
par convention pour des théories spécifiques peuvent faire autrement.
Par exemple, les interprétations standard de la géométrie représentent les points
par des urelements, mais représentent les droites par des ensembles de points.
Les interprétations génériques convertiront aussi les symboles de structure
en variables fixes (tandis que celles standard peuvent les définir par le langage
de la théorie des ensembles). Tout choix de valeurs fixes de tous les types et
symboles de structure, définit un choix de système. Lorsque le langage est vu comme un ensemble
(en particulier s'il est fini) ce qui est généralement le cas,
les modèles sont eux-mêmes des objets de la théorie des ensembles, dont la multiplicité
vient de la variabilité des types et des symboles de structures. Ceci permet d'intégrer
toutes les théories voulues dans une même théorie des ensembles, en rassemblant des
représentants de tous leurs modèles considérés dans un même modèle de la théorie
des ensembles. C'est pourquoi les modèles de la théorie des ensembles sont appelés des
univers. En adoptant la théorie des ensembles comme notre cadre conceptuel, ce
concept "d'interprétation" devient synonyme de choix (désignation) d'un modèle.
Other languages:
EN : 1. First foundations of
mathematics : 1.3. Form of theories:
notions, objects, meta-objects