1.D. La théorie des ensembles comme cadre unifié
Définisseurs de structure dans diverses théories
Appelons définisseur de structure tout symbole liant B qui
enregistre fidèlement la structure unaire (relation, resp. fonction)
définie par toute expression entrée (formule, resp. terme)
A sur un domaine E (type, classe ou ensemble ici fixé), à savoir
que son résultat S = (Bx, A(x)) peut restaurer cette
structure par un évaluateur V (symbole ou expression):
∀E x, V(S, x) = A(x).
Admettant l'utilisation de la négation
et la possibilité d'interpréter des booléens par des objets (dans un ensemble
à au moins deux objets, comme cela arrive souvent), le paradoxe de
Russell montre que l'ajout des deux exigences suivantes à un définisseur
de structure dans une théorie conduirait à une contradiction:
- Tous ces S appartiennent à E
- V peut apparaître dans l'expression A et utiliser x
n'importe comment dans ses arguments. Donc V(x,
x) est autorisé, ce qui est normal comme 1. garantit l'admissibilité
de tout V(S, S).
Enumérons les options restantes. La théorie des ensembles rejette 1. mais
conserve 2. Mais puisque 1. est rejeté, conserver 2. peut être un problème
ou non suivant les cas plus précis.
Toute théorie générique (dont les domaines des symboles liants sont les types)
peut se développer (comme sera expliqué en 4.11), par la construction
d'un nouveau type K donné comme l’ensemble de toutes les structures
définies par une expression fixe A pour toutes les combinaisons de
valeurs de ses paramètres, constitue un développement légitime de la théorie
(une construction). En effet, un symbole liant de domaine K abrège une
utilisation successive de symboles liants sur tous les paramètres de A.
Ici, A et le modèle l’interprétant viennent d'abord, puis l'ensemble
K de structures avec son évaluateur V sont créés en dehors:
A n'a pas de sous-terme de type K, donc n'utilise pas V.
La notion de structure dans 1MT
(théorie du modèle en logique du premier ordre), présente cette similitude avec
la notion d'ensemble en théorie des ensembles: dans 1MT, la classe de toutes les structures
de chaque type de symbole fixé (au-delà des constantes) n'est généralement pas
un ensemble, appelant "ensembles" de tels ensembles K (de celles définies
par une expression fixe avec des paramètres variables), et leurs sous-ensembles.
Cette similitude peut se formaliser en regroupant tous ces K du même type
de symbole (construits pour toutes les expressions possibles A) en un seul type
U, avec le même évaluateur V (ces A peuvent utiliser V
mais pas le domaine U). Cette fusion d'une infinité d'ensembles en un ne fait
que réécrire ce qu'on pouvait déjà faire sans cela, tant que les variables de
type U ne sont liées que sur un de ces "ensembles" K (ou de façon
équivalente un ensemble couvert par un nombre fini d'entre eux).
En théorie des ensembles, les domaines des symboles liants sont les ensembles.
Ainsi, au-delà de l'avantage simplificateur de supprimer les types, la théorie des
ensembles gagnera de la puissance par ses axiomes
renforçants qui reviennent à accepter plus de classes comme ensembles.
D'autres théories, que nous ignorerons dans la suite de ce travail, suivent des options plus audacieuses:
-
Conserver 1. et rejeter 2. sera montré cohérent par le paradoxe de Skolem (4.7)
mais serait largement artificiel.
-
Plus étrange encore est NF ("New Foundations", ainsi nommé comme il était nouveau
lors de sa première publication en 1937), combinant 1. avec une version allégée de 2.
restreignant la syntaxe possible de A pour interdire les occurrences de
(x∈x) ou de tout moyen de le définir.
- Le plus extrême est le lambda calcul, qui garde les deux points mais tolère la
contradiction qui en résulte en ignorant la logique booléenne avec son concept de
"contradiction". Cette "théorie" ne décrit aucun objet, mais seulement ses propres
termes, considérés comme des fonctions calculables. En tant que système de calcul,
ses contradictions sont des calculs qui continuent à tourner sans jamais donner
de résultat.
Le cadre unifié des théories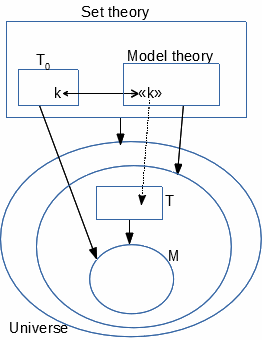
Comme l'arithmétique (et autres FOT), formaliser TT ou tout 1TT en tant
que théorie complète, requiert un axiome de second ordre
pour exclure les modèles non-standard avec des «expressions» et «preuves» pseudo-finies.
Or, le meilleur environnement pour de telles théories du second ordre (donnant une
apparence de détermination unique, non réelle), et aussi pour MT ou 1MT, est
l'insertion dans
une version suffisamment forte de la théorie des ensembles (qui peut définir la finitude: voir 4.6).
Cette insertion transformant les composants en variables libres qui ensemble désignent
le modèle, leur variabilité élimine la principale différence entre TT et 1TT, et entre MT et
1MT (une autre différence est que MT peut décrire des théories incohérentes). Ce
développement de la théorie des modèles à partir d'une version suffisamment forte de
la théorie des ensembles viendra dans les parties 3 et 4,
complétant le grand tour des fondements des mathématiques après la formalisation de la théorie
des ensembles (principalement par les parties 1 et 2).
Pour une théorie T ainsi décrite, soit T0 la théorie externe,
également insérée en théorie des ensembles, qui ressemble à une copie de T
comme tout composant
k de T0 a une copie comme objet servant de composant de T.
Dans une formalisation appropriée, T0 peut être défini à partir de T
comme formé des k tel que Univers⊨ ⌜k⌝∈T, ce qui signifie que la valeur de
la citation ⌜k⌝ interprétée dans l'univers, appartient à T.
Mais il n'y a pas de définition inverse générale, de T à partir d'un
T0 avec une infinité de composants, car un objet ne peut
pas être défini à partir d'une infinité donnée de méta-objets. Toute liste infinie
de composants de T0 doit répondre à une définition, pour
obtenir l'image idéalisée T de T0 en interprétant
cette définition dans l'univers. (La formule de définition doit être bornée pour
que T0 corresponde à la définition ci-dessus par ce T).
Ceci forme un cadre commode pour décrire les théories et leurs
modèles, unifiant les deux cadres précédents (ensembliste et modèle-théorique):
tous les travaux de T0 (expressions, preuves et autres
développements), ont des copies comme objets (en interprétant leurs citations)
décrits formellement par le développement
modèle-théorique de la théorie des ensembles comme travaux de la théorie T.
Dans le même univers, tout système M décrit comme modèle de T
est indirectement aussi un modèle (ensembliste) de T0.
Mais en tant que théorie du premier ordre, la théorie des ensembles ne peut
pas exclure les univers non standard, dont l'interprétation des FOT est non
standard (avec des objets pseudo-finis). Dedans, les discordances
suivantes entre T0 et T peuvent se produire:
- Tout T avec une infinité de composants a également des composants
non standard; mais T0 ne copie que ses composants standard.
Puis, un modèle de T0 peut ne pas être un modèle de
T faute de satisfaire un axiome non standard (pseudo-fini) de T.
- T peut être incohérent alors que T0 est cohérent,
par une contradiction non standard (pouvant utiliser ou non des axiomes non standard).
Un tel T n’a pas de modèle dans cet univers ; les modèles de
T0 peuvent soit n'exister qu'en dehors,
soit aussi dedans sans être un modèle de T pour la raison ci-dessus.
Ainsi comprises, les conditions de validité de ce cadre unifié sont
habituellement acceptées comme des hypothèses légitimes, en se concentrant sur
des théories bien décrites, interprétées dans des univers standard dont l'existence est
admise pour des raisons philosophiques.
La
théorie des ensembles comme cadre unifié d'elle-même
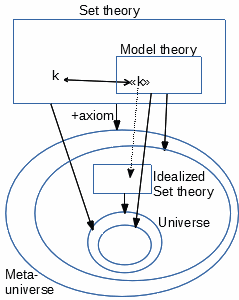
L'application de ce cadre unifié au choix d'une théorie des ensembles dans
le rôle de T0 (décrivant M et idéalisée comme objet
T) élargit les outils d'interprétation de la théorie des ensembles dans
elle-même (1.7). Comme T0 coexiste au même niveau avec
la théorie des ensembles servant de cadre, on peut les prendre comme copies
exactes l'une de l'autre (sans problème de standardité), ce qui revient à prendre
la même théorie des ensembles avec deux interprétations: M appelé "univers",
et l'interprétation cadre appelée "méta-univers ".
Mais le second théorème
d'incomplétude les fait différer comme suit. L'énoncé d'existence d'un univers d'une
théorie des ensembles donnée T (et donc aussi
l'énoncé plus fort de l'existence d'un univers standard), exprimé comme énoncé
ensembliste interprété dans le méta-univers, ne peut pas être un théorème
de T. Cela montre la nécessaire diversité des forces entre les théories
axiomatiques des ensembles utiles, qui sera commentée plus en détail en 2.C.
Le paradoxe de Zénon
Achille poursuit une tortue ; à chaque fois qu'il parcourt la
distance qui l'en sépare, celle-ci prend une nouvelle longueur
d'avance.
Vu d'une hauteur, un véhicule parti sur une route horizontale se
rapproche sans cesse de l'horizon.
Les particules sont envoyées dans les accélérateurs de plus en plus
près de la vitesse de la lumière.
Peuvent-ils atteindre leur but ?
Chaque exemple peut être vu de 2 manières:
- la vue «fermée» voit une extrémité atteignable;
- la vue «ouverte» ignore cette extrémité, mais ne voit que le
mouvement qui s'en approche indéfiniment sans jamais l'attendre.
Dans chaque exemple, une mesure physique du «coût» pour approcher
et éventuellement atteindre l'extrémité visée, décide quelle est sa
seule «vraie» lecture, suivant que ce coût serait fini ou infini (ce
qui peut différer des suppositions d'un observateur naïf).
Mais le monde des mathématiques, libre de toute mesure de coût
physique et où les objets ne font que jouer des rôles
conventionnels, peut accepter les 2 points de vue.
Chaque théorie générique pouvant utiliser des symboles liants sur des types,
elle considère les types comme des ensembles et «atteint la fin» de son modèle
qu'elle voit comme un tout «fermé». Mais tout cadre qui l'englobe (théorie du modèle
ou théorie des ensembles) échappe à cette totalité. Or, la théorie des ensembles a de
multiples modèles, d'un univers à un méta-univers (contenant plus d'ensembles: les
méta-ensembles, et de nouvelles fonctions entre eux) et ainsi de suite (un
méta-méta-univers ...). Pour refléter les possibilités illimitées d'échapper à tout
univers donné, on a besoin d'une théorie «ouverte» intégrant chaque univers comme
partie (passée) d'un univers ultérieur, formant une succession illimitée de réalités
croissantes, sans perspective sur son éventuelle totalité. Ce rôle de théorie ouverte
sera joué par la théorie des ensembles elle-même, par la manière dont ses
expressions ne lient
les variables que sur des ensembles.
Other languages:
EN : 1. First foundations of
mathematics : 1.D. Set theory as a unified framework