Set Theory and Foundations of Mathematics

About (purpose and author) - Foundations of physics - Other topics and links
Other languages : FR − ES − IT − RU − TR − LT

Cycle of foundations
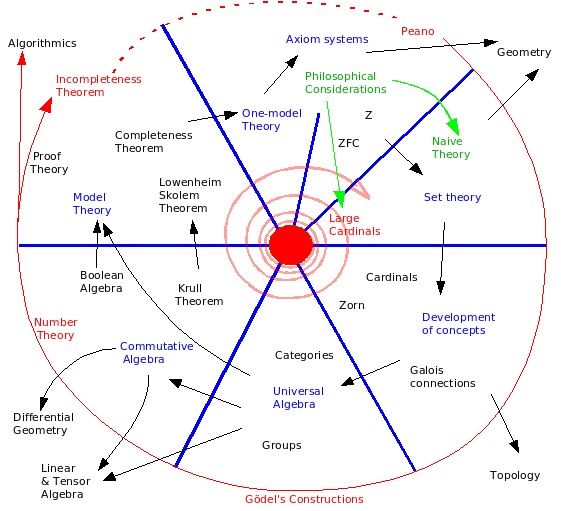
1. First foundations of mathematics (details) - all in 1 file (36 paper pages) - pdf version in 21 pages (roughly 14+7 - updated by automatic conversion from html).
1.1. Introduction to the foundations of mathematics
1.2. Variables, sets, functions and operations
1.3. Form of theories: notions, objects, meta-objects
1.4. Structures of mathematical systems
1.5. Expressions and definable structures
1.6. Logical connectives
1.7. Classes in set theory
1.8. Binders in set theory
1.9. Axioms and proofs
1.10. Quantifiers
1.11. Second-order universal quantifiers
More philosophy:
1.A. Time in model theory
1.B. Truth undefinability
1.C. Introduction to incompleteness
1.D. Set theory as a unified framework

2. Set theory - all in one file (40 paper pages), pdf (37 pages not updated).
A notation change was done away from standards (see why) : from their definition in 2.6, the notation for direct images of sets by a graph R changed from R∗ to R⋆, and that for preimages changed from R* to R⋆.
2.1. First axioms of set theory
2.2. Set generation principle
2.3. Currying and tuples
2.4. Uniqueness quantifiers
2.5. Families, Boolean operators on sets
2.6. Graphs
2.7. Products and powerset
2.8. Injections, bijections
2.9. Properties of binary relations
2.10. Axiom of choice
Philosophical aspects :
2.A. Time in set theory
2.B. Interpretation of classes
2.C. Concepts of truth in mathematics

3. Algebra 1 (all in one file)
3.1. Galois connections
3.2. Relational systems and concrete categories
3.3. Algebras
3.4. Special morphisms
3.5. Monoids and categories
3.6. Actions of monoids and categories
3.7. Invertibility and groups
3.8. Properties in categories
3.9. Initial and final objects
3.10. Products of systems (updated)
3.11. Basis
3.12. Composition of relations

4. Arithmetic and first-order foundations (all in one file : 30 paper pages)
4.1. Algebraic terms
4.2. Quotient systems
4.3. Term algebras
4.4. Integers and recursion
4.5. Presburger Arithmetic
4.6. Finiteness
4.7. Countability and Completeness
4.8. More recursion tools (draft)
4.9. Non-standard models of Arithmetic
4.10. Developing theories : definitions
4.11. Constructions
4.A. The Berry paradox

5. Second-order foundations
5.1. Second-order structures and invariants
5.2. Second-order logic
5.3. Well-foundedness
5.4. Ordinals and cardinals (draft)
5.5. Undecidability of the axiom of choice
5.6. Second-order arithmetic
5.7. The Incompleteness Theorem (draft)
More philosophical notes (uses Part 1 with philosophical aspects + recursion) :
Gödelian arguments against mechanism : what was wrong and how to do instead
Philosophical proof of consistency of the Zermelo-Fraenkel axiomatic system

6. Foundations of Geometry (draft)
6.1. Introduction to the foundations of geometry
6.2. Affine spaces
6.3. Duality
6.4. Vector spaces and barycenters
Beyond affine geometry
Euclidean geometry

7. Algebra 2 (draft)
Varieties
Polymorphisms and invariants
Relational clones
Abstract clones
Rings
(To be continued - see below drafts)

Galois connections (11 pdf pages). Rigorously it only uses parts 1 (without complements) and 2. Its position has been moved from 3 for pedagogical reasons (higher difficulty level while the later texts are more directly interesting). The beginning was moved to 2.11.

Monotone Galois connections (adjunctions)
Upper and lower bounds, infimum and supremum
Complete lattices
Fixed point theorem
Transport of closure
Preorder generated by a relation
Finite sets
Generated equivalence relations, and more
Well-founded relations

Index of special words, phrases and notations, with references

Drafts of more texts, to be reworked later

Dimensional analysis : Quantities and real numbers - incomplete draft text of a video lecture I wish to make on 1-dimensional geometry
Introduction to inversive geometry
Affine geometry
Introduction to topology
Axiomatic expressions of Euclidean and Non-Euclidean geometries
Cardinals

An alternative to Zorn's Lemma

Diverse texts ready but not classified

Pythagorean triples (triples of integers (a,b,c) forming the sides of a right triangle, such as (3,4,5))
Resolution of cubic equations
Outer automorphisms of S6

Contributions to Wikipedia

I wrote large parts of the Wikipedia article on Foundations of mathematics (Sep. 2012 - before that, other authors focused on the more professional and technical article Mathematical logic instead; the Foundations of mathematics article is more introductory, historical and philosophical) and improved the one on the completeness theorem.