1.1. Introduzione ai fondamenti della matematica
Che cos'è la matematica
La matematica è lo studio di sistemi di oggetti elementari, la cui unica natura tenuta
in considerazione è di essere esatti, non ambigui(due oggetti sono uguali o diversi, correlati o meno;
un'operazione dà un risultato esatto...). La matematica nel complesso può essere vista come
«la scienza di tutti i mondi possibili» di questo tipo (cioè di oggetti esatti).
I sistemi matematici sono concepiti come «esistenti» indipendentemente dal nostro mondo abituale
o da una particolare sensazione, nonostante ciò il loro studio richiede una qualche forma di rappresentazione.
Vari modi posso essere usati, che potrebbero essere equivalenti(cioè dare gli stessi risultati) ma con
diversi gradi di attinenza (efficenza) che potrebbero dipendere da diversi obiettivi. Le idee potrebbero
inizialmente apparire come intuizioni visive che potrebbero essere espresse da disegni o
animazioni, poi la loro articolazione potrebbe essere espressa a parole o con formule per un attento controllo,
esecuzione e comunicazione. Liberarsi dai limiti o bias di una specifica
forma di rappresentazione è una questione di sviluppare altre forme di rappresentazione,
e di esercitarsi nel tradurre concetti tra loro. L'avventura matematica
è piena di giochi di conversione tra forme di rappresentazione, che potrebbero riflettere
articolazioni tra i sistemi matematici stessi.
Teorie
La matematica è divisa in distinte branche a seconda del tipo di sistemi
presi in considerazione. Questi framework (sistemi di riferimento) di qualsiasi attività matematica
possono rimanere impliciti (con limiti vaghi), o formalmente specificati come teorie. Qualsiasi
teoria è lo studio di un - presumibilmente fissato - sistema che è il suo mondo di
oggetti, chiamati i suoi modelli. Ma ogni modello di una teoria potrebbe essere solo uno delle sue
possibili interpretazioni tra altri parimenti legittimi modelli. Per esempio,
parlando approssimativamente, tutti i fogli di carta sono sistemi di punti materiali, modelli
della stessa teoria Euclidea della geometria dei piani, ma indipendenti gli uni dagli altri.
La parola «teoria» potrebbe prendere diversi significati tra usi matematici e non matematici
(nel linguaggio comune e altre scienze).
Una prima distinzione è per natura (oggetti di tipo generale); l'altra distinzione,
è per intento (realismo vs. formalismo) verrà discussa in seguito.
Le teorie non matematiche descrivono approssimativamente o qualitativamente alcuni sistemi
o aspetti del mondo (campi d'osservazione) che eludono semplici descrizioni esatte.
Per esempio, descrizioni tipiche della chimica richiedono approssimazioni drastiche, raccogliendo
da osservazioni alcuni effetti arbitrari la cui deduzione dalla fisica quantistica
è tipicamente fuori la portata di calcoli diretti. La mancanza di una chiara distinzione
degli oggetti e delle loro proprietà induce al rischio di errori quando gli oggetti sono
approacciati nel tentativo di dedurre qualche proprietà da altre, come dedurre
una qualunque proprietà generale di un sistema da - potenzialmente indefinite - proprietà delle sue parti.
Le teorie della matematica pura, descrivendo solo sistemi esatti, possono tipicamente essere
protette dal rischio di essere «false», facendo uso di metodi propriamente rigorosi (regole formali)
progettati per il mantenimento della esatta conformità di teorie al loro designato modello.
Tra i due, le teorie della matematica applicata, come ad esempio le teorie della fisica
sono anche loro teorie matematiche ma i sistemi matematici che descrivono
sono intenti a idealizzate (semplificate) versioni di aspetti di certi sistemi del mondo reale
beché ne trascurino altri aspetti; a seconda della sua precisione,
questa idelizzazione (riduzione della realtà a una teoria della matematica applicata) permette anche questa
deduzioni corrette entro un certo margine d'errore.
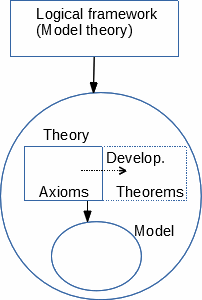Fondamenti e sviluppi
Qualsiasi teoria matematica, che descrive il/i suo/i modello/i, è fatta da un contenuto
ed è a sua volta descritto da un framework logico (quadro logico). Il contenuto di una teoria è fatto
da componenti i quali sono frammenti di descrizione (informazioni e concetti
descritti in 1.3). Una teoria inizia con una scelta di fondamenti fatta da un
framework logico e da una versione iniziale del suo contenuto (si spera piccolo, o almeno
descritto semplicemente). I componenti di questa versione iniziale sono ammessi come
primitivi.
Lo studio della teoria progredisce scegliendo alcuni dei suoi possibili
sviluppi: nuovi componenti risultanti dal suo (della teoria) corrente contenuto, al quale
possono essere aggiunti per formare il suo prossimo contenuto. Questi diversi contenuti, avendo lo
stesso significato (descrivendo essenzialmente gli stessi modelli), giocano il ruolo di
diverse presentazioni della stessa teoria.
Qualsiasi altro possibile sviluppo (non ancora scelto) può sempre essere aggiunto in seguito, visto che la parte
dei fondamenti che potrebbe generarlo rimane. Quindi, la totalità dei possibili sviluppi
di una teoria, indipendentemente dall'ordine scelto per processarli, già forma un tipo di
«realtà» che questi sviluppi esplorano.
Per esprimere le proprietà dei suoi modelli, il contenuto di una teoria include una lista di
dichiarazioni, che sono formule prese per vere quando interpretate in qualsiasi modello.
Dichiarazioni primitive sono chiamate assiomi. Le dichiarazioni che li seguono sono chiamate teoremi
e sono aggiunti al contenuto attraverso lo sviluppo della teoria, sotto la condizione che siano dimostrati
(dedotti) dai precedenti: questo assicura loro di essere veri in tutti i modelli,
a patto che lo fossero anche i precedenti. I teoremi possono essere usati in ulteriori sviluppi
allo stesso modo degli assiomi.
Una teoria è consistente se i suoi teoremi non si contraddicono mai l'un l'altro.
Teorie inconsistenti non possono aver alcun modello, non potendo una dichiarazione essere vera e falsa
nello stesso sistema.
Il Teorema della Completezza (1.9,
4.6) mostrerà che la
gamma di tutti i possibili teoremi riflette precisamente la più interessante realtà
della diversità dei modelli, che appunto esiste per qualsiasi teoria consistente.
Altre tipologie di sviluppo (definizioni e costruzioni) che aggiungono altri
componenti oltre alle dichiarazioni, saranno descritti in 1.5, 4.8 e 4.9.
Ci sono possibili gerarchie tra teorie, dove alcune possono
giocare un ruolo fondazionale per altre. Ad esempio, i fondamenti di
diverse teorie potrebbero avere una parte comune che forma una teoria più semplice,
i quali sviluppi sono applicabili a tutti.
Un lavoro fondamentale
è di sviluppare, da una semplice base iniziale, un conveniente corpo di conoscenze
utile a una più completa "fondazione", dotata di strumenti efficienti
che aprano vie più dirette a ulteriori sviluppi interessanti.
Platonismo vs Formalismo
La matematica, o ogni teoria, può essere approcciata in due modi (come discusso in seguito
in 1.9):
- Il Platonico o realistico punto di vista, considera il regno matematico
- o alcuni particolari sistemi descritti - come realtà pre-esistenti da esplorare (o
ricordare, secondo Plato). Questo è l'approccio dell'intuizione che immaginando cose
fiuta il loro ordine prima di formalizzarle.
- Un formalistico o logicisto punto di vista si focalizza sul linguaggio, rigore
(regole sintattiche) e aspetti dinamici di una teoria, partendo dalla
sua fondazione formale, e seguendo le regole dello sviluppo.
Molti filosofi della
matematica sostengono concezioni obsolete di quei punti di vista formando una molteplicità
di opposte convinzioni (verità candidate) sulla reale natura della matematica. Ma dopo averle esaminate,
rimangono solo questi due necessari e complementari punti di vista,
la cui attinenza varia in certe parti a seconda dell'argomento :
Dalle sue abilità limitate, il pensiero umano non può operare direttamente in modo completamente realistico
sistemi infiniti (o finiti ma con grandezza illimitata), ma richiede
una qualche logica per l'estrapolazione, più o meno equivalente a ragionamenti formali
sviluppati da qualche fondazione ; questo lavoro di formalizazione può prevenire
possibili errori d'intuizione. Inoltre, gli oggetti matematici non possono formare una completa totalità,
ma un sempre temporaneo, regno in espansione, la cui precisa
forma è una sembianza relativa alla scelta di formalizzazione.
Ma oltre all'incoveniente nell'esprimere dimostrazioni, un punto di vista
puramente formalistico non può comunque reggere a sé stante perché la chiarezza e l'autosufficienza di qualsiasi
possibile fondazione (posizione iniziale con regole di sviluppo formali), rimane
relativa: qualsiasi punto di partenza è stato necessariamente scelto arbitrariamente, preso e motivato da
una più larga prospettiva su realtà matematiche; deve essere definito in un qualche modo
intuitivo e presumibilmente significativo, ammettendo implicitamente la sua propria 'fondazione', visto che
ogni tentativo di specificare quest'ultima porterebbe a un percorso d'interminabile regressione, la cui realistica
preesistenza necessiterebbe di essere ammessa.
Il ciclo dei fondamenti
Nonostante la semplicità della natura degli oggetti matematici, il generale
fondamento di tutta la matematica si scopre essere alquanto complesso (anche se
non tanto quanto la teoria fisica del tutto). Di fatto, è in sé stesso
un argomento della matematica, pertanto una branca della matematica, chiamata logica matematica.
Come qualsiasi altra branca, è piena di definizioni e teoremi
riguardanti sistemi di oggetti. Ma come oggetto ha la forma generale delle teorie e sistemi
che potrebbe descrivere, fornisce il framework generale di tutte le branche della matematica...
incluso sé stessa.
E per fornire il framework o fondamento di tutti i considerati fondamenti
(diversamente da qualsiasi opera matematica che segue da un presunto fondamento),
non sembra come un preciso punto iniziale,
ma una specie di largo ciclo composto di passi più o meno difficili. Tuttavia questo
ciclo di fondamenti gioca veramente un ruolo fondazionale per la matematica, dimostrando
framworks rigorosi e molti concetti utili a distinte branche della matematica
(strumenti, ispirazioni e risposte a distinte domande filosofiche).
(Questo è simile a un dizionario che definisce ogni parola da un'altra parola, o simile a
un'altra scienza di sistemi finiti:programmazione informatica. Difatti i computers
possono essere usati semplicemente, sapendo cosa fare, ma non come funziona; il loro funzionamento
è basato su software che è statto scritto in un linguaggio, per poi essere compilato da un
altro software, il tutto su hardware e processori i quali design e produzione stessi
erano computer-assisted. Ed è molto meglio che alla nascita del di questo campo di studi.)
E' dominato da due teorie:
-
Teoria degli insiemi descrive l'universo di «tutti gli oggetti
matematici», dal più semplice al più complesso come sistemi infiniti
(in un linguaggio finito). Può essere approssimativamente visto come una sola teoria,
ma nel dettaglio avrà infite varietà di possibili varianti
(di fatto diverse l'un l'altra).
-
Teoria del modelli è lo studio delle teorie (il loro formalismo come sistemi
di simboli), e sistemi (modelli possibili di teorie). La teoria delle dimostrazioni
completa il tutto descrivendo sistemi formali di regole di dimostrazioni. Mentre queste teorie
sono tipicamente intese come argomenti generali (che ammettono varianti di concetti), la loro
combinazione può essere specificata in versioni precise (teorie matematiche)
chiamate framework logici(logical frameworks), dando ad ognuno una precisa forma (un format)
di espressione per un'ampia gamma di teorie possibili, e un format nel quale tutte le prove
in qualsiasi di queste teorie possono in principio essere espresse. C'è un
essenziale unico principale framework logico chiamato logica del primo ordine,(first-order logic)
nel quale i concetti di teoria, teorema (come dichiarazione dimostrabile) e
consistenza di ogni teoria, trovano la loro naturale definizione matematica;
ma anche altri framework logici sono a volte necessari.
Ognuno è il naturale framework per formalizzare gli altri: ogni teoria degli insiemi è formalizzata
come una teoria descritta dalla teoria dei modelli; l'ultima meglio viene come uno sviluppo dalla teoria degli insiemi
(definendo teorie e sistemi come oggetti complessi) piuttosto che direttamente come una teoria a sé stante.
Entrambe le connessioni devono essere considerate separatamente: entrambi i ruoli della teoria degli insiemi, come una
base e un oggetto di studi della teoria dei modelli, devono essere distinti. Ma queste
formalizzazioni necessiteranno di un lungo lavoro per essere completate.
Other languages:
EN : Introduction
to the foundation of mathematics
FR :
Introduction au fondement
des mathématiques