1.1. Introduction to the foundations of mathematics
What is mathematics
Mathematics is the study of systems of elementary objects, whose only considered
nature is to be exact, unambiguous (two objects are equal or different, related or not;
an operation gives an exact result...). Mathematics as a whole can be seen as
«the science of all possible worlds» of this kind (of exact objects).
Mathematical systems are conceived as «existing» independently of our usual world
or any particular sensation, but their study requires some form of representation.
Diverse ways can be used, that may be equivalent (giving the same results) but with
diverse degrees of relevance (efficiency) that may depend on purposes. Ideas may
first appear as more or less visual intuitions which may be expressed by drawing or
animations, then their articulations may be expressed in words or formulas for careful
checking, processing and communication. To be freed from the limits or biases of a
specific form of representation, is a matter of developing other forms of representation,
and exercizing to translate concepts between them. The mathematical
adventure is full of plays of conversions between forms of representation,
which may reflect articulations between mathematical systems themselves.
Theories
Mathematics is split into diverse branches according to the kind of systems
being considered. These frameworks of any mathematical work may either
remain implicit (with fuzzy limits), or formally specified as theories. Each
theory is the study of a supposedly fixed system that is its world of
objects, called its model. But each model of a theory may be just one of its
possible interpretations, among other possibly legitimate models. For example,
roughly speaking, all sheets of paper are systems of material points, models
of the same theory of Euclidean plane geometry, but independent of each other.
The word «theory» may take diverse meanings between uses, from mathematical
ones to those of ordinary language and other sciences.
Let us first present the distinction by nature (general kind of objects); the other distinction,
by intent (realism vs. formalism) is introduced below and in 1.9.
Non-mathematical theories describe roughly or qualitatively some systems
or aspects of the world (fields of observation) which escape exact self-sufficient
description. For example, usual descriptions of chemistry involve drastic approximations,
recollecting some rough accounts of seemingly arbitrary effects and laws, whose
deductions from quantum physics are often out of reach of direct calculations. The
lack of clear distinction of objects and their properties induces risks of mistakes when
approaching them and trying to infer some properties from others, such as to
infer some global properties of a system from likely, fuzzy properties of its parts.
Pure mathematical theories, only describing exact systems, can usually be
protected from the risk to be «false», by use of rigorous methods (formal rules)
designed to ensure preserving the exact conformity of theories to their intended models.
In between both, applied mathematical theories, such as theories of physics
are also mathematical theories but the mathematical systems they
describe are meant as idealized (simplified) versions of aspects of given
real-world systems while neglecting other aspects; depending on its accuracy,
this idealization (reduction to mathematics) also allows for correct deductions
within accepted margins of error.
 Foundations and developments
Foundations and developments
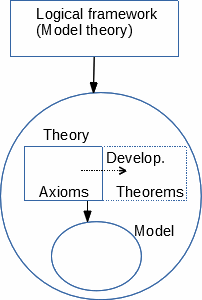
Any mathematical theory, which describes its model(s), is made of a content
and is itself described by a logical framework. The content of a theory is made
of components which are pieces of description (concepts and information we shall
describe in 1.3). A theory starts with a choice of foundation made of a
logical framework and an initial version of its content (hopefully rather small, or at
least simply describable). The components of this initial version are qualified as
primitive.
The study of the theory progresses by choosing some of its possible
developments : new components resulting from its current content
(by rules also described by the logical framework), and
that can be added to it to form its next content. These different contents, having
the same meaning (describing the essentially same models), play the role of
"different presentations of the same theory".
Any other possible development (not yet chosen) can still be added later, as the
part of the foundation that could generate it remains. Thus, the totality of
possible developments of a theory, independent of the order chosen to process
them, already forms a kind of «reality» that these developments explore.
To express the properties of its models, each theory includes a list of
statements, which are formulas meant as true when interpreted in any model.
Its primitive statements are called axioms. Further statements called theorems
are added by development to the content, under the condition that they are proven
(deduced) from previous ones : this ensures them to be true in all models,
provided that previous ones were. Theorems can then be used in further
developments in the same way as axioms.
A theory is consistent if its theorems will never contradict each other.
Inconsistent theories cannot have any model, as the same statement cannot be
true and false on the same system. The Completeness Theorem (1.9, 1.10,
4.7) will show that the
range of all possible theorems precisely fits the more interesting reality
of which statements stay true across the range of all models (which indeed exist for
any consistent theory).
Other kinds of developments (definitions and constructions) adding other
components beyond statements, will be described in 1.5, 1.D, 4.10 and 4.11.
There are possible hierarchies between theories, where some can
play a foundational role for others. For instance, the foundations of
several theories may have a common part forming a simpler theory,
whose developments are applicable to all.
A fundamental work
is to develop, from a simple initial basis, a convenient body of knowledge
to serve as a more complete "foundation", endowed with efficient tools
opening more direct ways to further interesting developments.
Platonism vs Formalism
Mathematics, or each theory, may be approached in two ways (detailed
in 1.9):
- The Platonic or realistic view, considers the mathematical realm
or some particular described systems, as preexisting realities to be explored (or
remembered, according to Plato). This is the approach of intuition which by imagining
things, smells their order before formalizing them.
- A formalistic or logicist view focuses on language, rigor
(syntactic rules) and dynamical aspects of a theory, starting
from its formal foundation, and following the rules of development.
Many philosophers of
mathematics carry obsolete conceptions of such views as forming a list of multiple
opposite beliefs (candidate truths) on the real nature of mathematics. But after
examination, just remain these two necessary and complementary views,
with diverse shares of relevance depending on topics.
By its limited abilities, human thought cannot operate in any fully
realistic way over infinite systems (or finite ones with unlimited size), but requires
some kind of logic for extrapolation, roughly equivalent to formal reasonings
developed from some foundations ; this work of formalization can prevent
possible errors of intuition. Moreover, mathematical objects cannot form any
completed totality, but only a forever temporary, expanding realm, whose precise
form is an appearance relative to a choice of formalization.
But beyond its inconvenience for expressing proofs, a purely
formalistic view cannot hold either because the clarity and self-sufficiency
of any possible foundation (starting position with formal development rules), remain
relative: any starting point had to be chosen somehow arbitrarily, taken from and
motivated by a larger perspective over mathematical realities; it must be defined in some
intuitive, presumably meaningful way, implicitly admitting its own foundation, while any
try to specify the latter would lead to a path of endless regression, whose realistic
preexistence would need to be admitted.
The cycle of foundations
The general foundation of all mathematics is itself a mathematical study, thus a
branch of mathematics, called mathematical logic. Despite the simplicity
of nature of mathematical objects, it turns out to be quite complex (though not
as bad as a physics theory of everything): by describing the general form of
theories and systems they may describe, it forms the general framework of all
branches of mathematics... including itself. So providing the foundation of each
considered foundation (unlike ordinary mathematical works that go forward from
an assumed foundation), it does not form a precise starting point, but a wide
loop composed of easier and harder steps. Still this cycle truly plays a foundational
role for mathematics, providing to its diverse branches many useful concepts
(tools, rigor, inspirations and answers to diverse philosophical questions).
(This is similar to the use of dictionaries defining each word by other words, or to this
other science of complex exact systems: computer programming. Indeed computers
can be simply used, knowing what you do but not why it works; their working
is based on software that was written in some language, then compiled by
other software, and on the hardware and processor whose design and production
were computer assisted. And this is much better in this way than at the birth of this
field.)
It is dominated by two theories:
-
Set theory describes the universe of «all mathematical
objects», from the simplest to the most complex such as infinite
systems (in a finite language). It can roughly be seen as one theory,
but in details it will have an endless diversity of possible variants
(indeed differing from each other).
-
Model theory is the study of theories (their formalisms as systems of
symbols), and systems (possible models of theories). Proof theory
completes this by describing formal systems of rules of proofs. While model theory
is usually meant as a general topic (admitting variants of concepts), it can
be specified into precise versions, thus mathematical theories called logical
frameworks, each giving a precise format of expression for a wide range
of possible theories, and (if completed by proof theory) a format in which all
proofs from any of these theories can in principle be expressed. There is an
essentially unique main logical framework called first-order logic,
by which the concepts of theory, theorem (i.e. provable statement) and
consistency of each theory, find their natural mathematical definitions;
but other logical frameworks are sometimes needed too.
Each one is the natural framework to formalize the other: each set theory is formalized
as a theory described by model theory; the latter better comes as a development from
set theory (defining theories and systems as complex objects) than directly as a theory.
Both connections must be considered separately: both roles of set theory, as a
basis and an object of study for model theory, must be distinguished. But these
formalizations will take a long work to complete.
Other languages:
FR :
Introduction au fondement
des mathématiques
 Foundations and developments
Foundations and developments Foundations and developments
Foundations and developments