1.D. Set theory as a unified framework
Structure definers in diverse theories
Let us call structure definer any binder B which faithfully records the unary
structure (relation, resp. function), defined by any input expression (formula, resp. term)
A on some range E (type, class or set here fixed), i.e. its result S =
(Bx, A(x)) can restore this structure by an evaluator V
(symbol or expression) : ∀E x,
V(S, x) = A(x).
Admitting the use of negation and the possibility to interpret
Booleans by objects (in a range with at least 2 objects, which is often
the case), Russell's paradox shows that adding both following requirements on
a structure definer in a theory would lead to contradiction :
- All such S belong to E
- V can occur in the expression A and use x anyhow in
its arguments. So V(x, x) is allowed, which is expected as 1.
ensures the definiteness of any V(S, S).
Let us list the remaining options. Set theory rejects 1. but keeps 2. But since 1.
is rejected, keeping 2. may be or not be an issue depending on further details.
In the construction (1.5) of a type K of structures defined by a formula A,
a binder with range K abbreviates a successive use of binders
on all the parameters of A. Here A and the interpreting model
come first, then the range K of structures with its evaluator V are
created outside them : A has no sub-term with type K, thus does
not use V.
The notion of "structure" in 1MT
(one-model theory in first-order logic) has this similarity with the notion of set
in set theory : in 1MT, the class of all structures of any fixed symbol type (beyond
constants) is usually not a set, calling "sets" such ranges K (of those
with a fixed defining expression and variable parameters) and their subsets.
This similarity can be formalized by gathering all such K of the same symbol
type (constructed by all possible expressions A) into a single type U,
with the same evaluator V (those A might use V but not the range
U). This merging of infinitely many ranges into one, merely re-writes what can
be done without it, as long as variables of type U are only bound on one of
these "sets" K (or equivalently, a range covered by finitely many of them).
In set theory, the ranges of binders are the sets. Thus, beyond its simplifying
advantage of removing types, set theory will get more power by its strengthening axioms
which amount to accept more classes as sets.
Other theories, which we shall ignore in the rest of this work, follow more
daring options:
- Keeping 1. and rejecting 2. will be shown consistent by
Skolem's Paradox (4.7)
but would be quite unnatural.
-
Even weirder is NF
("New Foundations", so called as it was new when first published in 1937),
combining 1. with a lighter version of 2. restricting the syntax of A
to forbid occurrences of (x∈x) or any way to define it.
- The most extreme is lambda
calculus, that keeps both points but
tolerates the resulting contradiction by ignoring Boolean logic with its
concept of "contradiction". This "theory" does not describe any object but
only its own terms, seen as computable functions. As a computation system,
its contradictions are computations which keep running never giving any
result.
The unified framework of theories
Like arithmetic (and other FOT), to formalize TT or any 1TT as a complete theory,
requires a second-order
axiom to exclude non-standard models with pseudo-finite
«expressions» and «proofs». Now, the best environment for such second-order
theories (giving an appearance of unique determination, though not a real one),
and also for MT or 1MT, is the
insertion
in a strong enough version of set theory (which can define finiteness: see 4.6).
As this insertion turns components into free variables which together designate
the model, their variability removes the main difference between TT and 1TT, and
between MT and 1MT (another difference is that MT can describe inconsistent theories).
This development of model theory from a strong enough version of set theory will
come in parts 3 and 4, completing the grand tour of the foundations of mathematics
after the formalization
of set theory (mainly by parts 1 and 2).
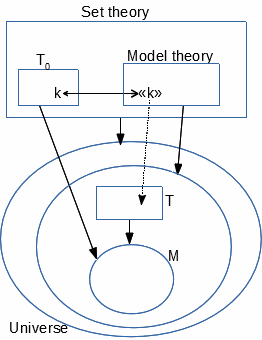Given a theory T so described, let T0 be the external
theory, also inserted in set theory, which looks like a copy of T as any
component k
of T0 is the copy of an object serving as a component of T.
In a suitable formalism, T0 can be defined from T as made of
the k such that Universe⊨ ⌜k⌝∈T, i.e. the value of the quoting term
⌜k⌝ interpreted in the universe belongs to T.
But there is no general
inverse definition, of T from a T0 with infinitely many
components, as an object cannot be defined from a given infinity of
meta-objects. Any infinite list of components of T0 needs to fit
some definition, to get the idealized image T of T0 by
interpreting that definition in the universe. (The defining formula must be bounded for
T0 to match the above definition from this T).
This forms a convenient framework for describing theories and their models,
unifying both previously mentioned set-theoretical and model-theoretical frameworks :
all works of the theory T0 (expressions, proofs and other
developments), have copies as objects (by interpreting their quotes) formally
described by the model theoretical development of set theory as works of the
theory T. In the same
universe, any system M described as a model of T is indirectly
also a (set-theoretical) model of T0.
But as a first-order theory, set theory cannot exclude non-standard universes, whose
interpretation of FOTs is non-standard (with pseudo-finite objects). There, the
following discrepancies between T0 and T may occur :
- Any T with an infinity of components also has non-standard
ones; but T0 only copies its standard components.
Then a model of T0 may fail to be a model of T by not fitting
some non-standard axioms of T.
- T may be inconsistent while T0 is consistent, due to a
non-standard contradiction (may it use non-standard axioms or only standard ones).
Such a T has no model in this universe, letting models of T0
either only exist outside it, or also in it with the above described failure to be a model
of T.
So understood, the validity conditions of this unified framework are usually accepted as
legitimate assumptions, by focusing on well-described theories, interpreted in standard
universes whose existence is admitted on philosophical grounds.
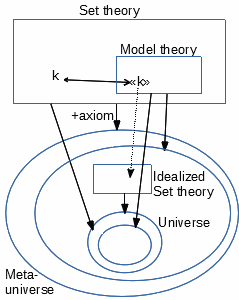Set theory as its own unified framework
Applying
this unified framework to the choice of a set theory in the role of T0
(describing M and idealized as an object T), expands the tools of interpretation of set theory into itself
(1.7). As T0 co-exists at the same level with the set theory serving as
framework, they can be taken as exact copies of each other (with no standardness issue),
which amounts to taking the same set theory with two interpretations : M called
"universe", and the framework interpretation called "meta-universe".
But the second
incompleteness theorem makes them differ as follows. The statement of existence of
a universe of any given set theory T (and thus also the stronger
statement of existence of a standard one), expressed as a set theoretical statement
interpreted in the meta-universe, cannot be a theorem of T. This shows the
necessary diversity of strengths between useful axiomatic set
theories, which will be further commented in 2.C.
Zeno's Paradox
Achilles runs after a turtle; whenever he crosses the distance to
it, the turtle takes a new length ahead.
Seen from a height, a vehicle gone on a horizontal road approaches
the horizon.
Particles are sent in accelerators closer and closer to the speed of
light.
Can they reach their ends ?
Each example can be seen in two ways:
- the «closed» view, sees a reachable end;
- the «open» view ignores this end, but only sees the movement
towards it, never reaching it.
In each example, a physical measure of the «cost» to approach and
eventually reach the targeted end, decides which view is «true», according
to whether this cost would be finite or infinite (which may differ from the first
guess of a naive observer). But the realm of mathematics, free from all
physical costs and where objects only play roles, can accept both
views.
As each generic theory can use binders over types, it sees types as wholes (sets)
and «reaches the end» of its model seen as «closed». But any framework encompassing
it (one-model theory or set theory) escapes this whole. Now set theory has multiple
models, from a universe to a meta-universe (containing more sets : meta-sets, and
new functions between them) and so on (a meta-meta-universe...). To reflect the
endless possibilities of escaping any given universe, requires an «open» theory
integrating each universe as a part (past) of a later universe, forming an endless
sequence of growing realities, with no view of any definite totality. The role of
this open theory is played by set theory itself, with the way its expressions only bind variables on sets.
Other languages:
FR :
Le cadre ensembliste unifié