1.1. Introduction aux fondements des mathématiques
Mathématiques
Les mathématiques sont l'étude des systèmes d'objets élémentaires,
dont la seule nature considérée est d'être exacts, sans ambiguïté (deux
objets sont égaux ou différents, reliés ou non ; une opération donne un
résultat exactement...). Les mathématiques dans leur ensemble peuvent être vus
comme «science de tous les mondes possibles» de cette espèce (faits
d'objets exacts).
Les systèmes mathématiques sont conçus comme «existant»
indépendamment de notre monde habituel ou de toute sensation particulière,
mais leur étude nécessite une certaine forme de représentation.
Diverses méthodes peuvent être utilisées, pouvant être équivalentes
(donnant les mêmes résultats) mais avec divers degrés de pertinence
(efficacité) pouvant dépendre des objectifs. Les idées apparaissent
habituellement comme intuitions plus ou moins visuelles exprimables
par des figures ou animations, puis leurs articulations peuvent s'exprimer
en mots ou formules pour être attentivement vérifiées, traitées et communiquées.
Pour se libérer des limites ou biais d'une forme de représentation particulière, il
suffit de développer d'autres formes de représentation, et de s'exercer à traduire
les concepts d'une forme à l'autre. L'aventure mathématique est pleine de jeux
de conversions entre diverses formes de représentation, qui peuvent refléter les
articulations entre les systèmes mathématiques eux-mêmes.
Théories
Les mathématiques se divisent en diverses branches suivant le type de système considéré.
Ces cadres de tout travail mathématique peuvent rester implicites (avec des limites
floues), ou bien être spécifiés formellement en tant que théories. Chaque
théorie est l'étude d'un système (son monde d'objets) supposé fixé,
appelé son modèle. Mais chaque modèle d'une théorie peut n'être qu'une
de ses interprétations possibles, parmi d'autres modèles possiblement
légitimes. Par exemple, en gros, toutes les feuilles de papier sont
des systèmes de points matériels, modèles de la même théorie de
la géométrie Euclidienne plane, mais indépendants les uns des autres.
Le mot «théorie» peut prendre divers sens suivant les utilisations, de celles mathématiques
à celles du langage ordinaire et d'autres sciences. Voici d'abord la
distinction suivant leur nature (la sorte générale d'objets); l'autre distinction, par
l'intention (réalisme contre formalisme), est introduite plus bas et en 1.9.
Les théories non-mathématiques décrivent grossièrement ou
qualitativement des systèmes ou aspects du monde (domaines d'observation),
qui échappent à la description simple et exacte. Par exemple, les descriptions
habituelles de la chimie utilisent des approximations drastiques, rassemblant
de grossières descriptions d'effets et de lois d'apparence arbitraires et dont la déduction
de la physique quantique est souvent hors de portée des calculs directs.
Le manque de distinction claire des objets et de leurs propriétés induit des risques
d'erreurs en les approchant et en essayant de déduire certaines propriétés à partir
d'autres propriétés, telles que de déduire certaines propriétés globales d'un
système à partir de propriétés floues probables de ses parties.
Les théories de mathématiques pures, décrivant des systèmes exacts, peuvent
habituellement être protégées du risque d'être «fausses», par l'usage de méthodes
rigoureuses (règles formelles) conçues pour préserver la conformité exacte
des théories à leurs modèles voulus.
Entre les deux, les théories de mathématiques appliquées, telles que les
théories physiques, sont aussi des
théories mathématiques, mais les systèmes mathématiques qu'elles décrivent sont
conçus comme versions idéalisées (simplifiées) d'aspects de systèmes donnés du
monde extérieur, négligeant d'autres aspects; suivant sa précision,
cette idéalisation (réduction à des mathématiques) permet également des
déductions correctes dans des marges d'erreur acceptées.
Fondements et développements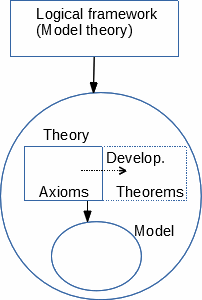
Toute théorie mathématique, décrivant son/ses modèle(s), est faite d’un
contenu et est elle-même décrite par un cadre logique.
Le contenu d'une théorie est fait de composants qui sont des éléments de
description (concepts et informations, décrits en 1.3). Une théorie démarre par le
choix d'un fondement formé d'un cadre logique et d'une version initiale
du contenu (de préférence petite ou au moins simplement descriptible). Les
composants de cette version initiale sont qualifiés de primitifs.
L'étude de la théorie progresse en choisissant certains de ses développements
possibles : de nouveaux composants qui résultent de son contenu actuel (par des
règles aussi décrites par le cadre logique), et peuvent lui être ajoutés pour
former son contenu suivant. Ces différents contenus, ayant la même
signification (décrivant essentiellement les mêmes modèles), jouent le rôle
de "présentations différentes de la même théorie".
Les autres développements possibles (non encore choisis) pourront
toujours être effectués plus tard, car la partie du fondement qui
pouvait les engendrer subsiste. Dès lors la totalité des développements
possibles d'une théorie, indépendante de l'ordre choisi pour les effectuer,
forme déjà une sorte de «réalité» que ces développements explorent.
Pour exprimer les propriétés de ses modèles, chaque théorie
comprend une liste d'énoncés qui sont des formules annoncées
comme vraies dans chaque modèle où elles sont interprétées. Ses énoncés
primitifs sont appelés axiomes. D'autres énoncés appelés théorèmes
s'ajoutent au contenu par développement, à la condition qu'ils soient prouvés
(déduits) à partir des précédents: ceci garantit qu'ils soient vrais dans tous les
modèles, du moment que les précédents l'étaient. Les théorèmes sont alors
utilisables dans les développements suivants au même titre que les axiomes.
Une théorie est cohérente (ou consistante)
si ses théorèmes ne se contrediront jamais. Les théories incohérentes ne
peuvent avoir aucun modèle, un même énoncé ne pouvaut être vrai et
faux sur un même système.
Le théorème de complétude (1.9, 1.10, 4.7) montrera que l'ensemble
de tous les théorèmes possibles suit précisément la réalité plus intéressante
de quels énoncés restent vrais dans tous les modèles (lesquels existent
pour toute théorie cohérente).
Les autres sortes de développements (définitions et constructions) ajoutant
d'autres composants au-delà des énoncés, seront décrits en 1.5, 1.D, 4.10 et 4.11.
Il y a des hiérarchies possibles entre théories, certaines pouvant jouer un
rôle fondateur pour d'autres. Notamment, les fondements de plusieurs
théories peuvent avoir une partie commune formant une théorie plus
simple, dont les développements sont applicables à toutes.
Un travail fondamental est de développer, à partir d'une base
initiale simple, un corps de connaissances commodes pour servir de
"fondement" plus complet, muni d'outils efficaces ouvrant des voies
plus directes vers d'autres développements intéressants.
Platonisme vs Formalisme
Les mathématiques, ou chaque théorie, peuvent être abordées de deux manières
(détaillées en 1.9).
- Le point de vue platonicien ou réaliste
considère le monde mathématique ou certains systèmes étudiés, comme réalités
mathématiques préexistantes à explorer (ou à se ressouvenir, d'après Platon).
C'est l'approche de l'intuition qui, en imaginant des choses, sent leur
ordre avant de les formaliser.
- Le point de vue formaliste ou logiciste se concentre sur le
langage, la rigueur (règles syntaxiques) et les aspects dynamiques d'une théorie,
en partant de son fondement formel, et en suivant les règles de développement.
De nombreux philosophes des
mathématiques ont des conceptions obsolètes de telles idées comme formant
une liste de multiples croyances opposées (vérités candidates) sur la nature réelle
des mathématiques. Mais après examen, il ne reste que ces deux approches
nécessaires et complémentaires, avec diverses parts de pertinence suivant les sujets:
Par ses capacités limitées, la pensée humaine ne peut pas opérer d'une manière
pleinement réaliste sur les systèmes infinis (ou des systèmes finis de
taille illimitée), mais nécessite une sorte de logique d'extrapolation, grossièrement
équivalente à des raisonnements formels développés à partir de certains fondements; ce
travail de formalisation permet d'éviter d'éventuelles erreurs de l'intuition.
De plus, les objets mathématiques ne peuvent pas former une totalité achevée,
mais seulement un domaine toujours temporaire, en expansion,
dont la forme précise est une apparence relative à un choix de formalisation.
Mais au-delà de son incommodité à exprimer les preuves, une vision purement
formaliste ne serait pas non plus tenable car la clarté et l’autosuffisance de tout
fondement possible (position de départ avec des règles de développement formelles)
restent relatives: tout point de départ a dû être choisi plus ou moins arbitrairement,
issu de et motivé par une perspective plus large sur les réalités mathématiques; il
doit être défini d'une manière intuitive, supposément claire, admettant implicitement
son propre fondement, car toute tentative de préciser ce dernier conduirait à une
régression sans fin, dont la préexistence réaliste devrait être admise.
Le cycle des fondements
Le fondement général de toutes les mathématiques est lui-même une étude
mathématique, donc une branche des mathématiques appelée la logique
mathématique. Malgré la simplicité de nature des objets mathématiques, il
s'avère assez complexe (quoique moins qu'une théorie du tout de la physique):
en décrivant la forme générale des théories et des systèmes qu'elles peuvent
décrire, il forme le cadre général de toutes les branches des mathématiques...
lui-même inclus. Ainsi fournissant le fondement de chaque fondement
considéré (à l'inverse des travaux mathématiques ordinaires avançant
à partir d'un fondement admis), il ne forme pas un point de départ précis,
mais une vaste boucle composée d'étapes plus ou moins difficiles.
Néanmoins, ce cycle joue bien un rôle fondateur pour les mathématiques,
fournissant à ses diverses branches de nombreux concepts utiles
(outils, rigueur, inspirations et réponses à diverses questions philosophiques).
(Cette situation ressemble au rôle des dictionnaires définissant chaque mot par
d'autres mots, ou à cette autre science des systèmes complexes exacts: l'informatique. On
peut en effet simplement utiliser les ordinateurs, sachant ce qu'on fait mais non
pourquoi cela fonctionne; leur fonctionnement se base sur des logiciels qui furent
rédigés dans un certain langage puis compilés par d'autres logiciels, et sur le
matériel et le processeur dont la conception et la fabrication furent assistées par
ordinateur. Et c'est nettement mieux ainsi qu'à la naissance de cette discipline.)
Il est dominé par deux théories:
-
La théorie des ensembles étudie l'univers de «tous les
objets mathématiques», des plus simples aux plus complexes comme les
systèmes infinis (dans un langage fini). Elle peut se voir en gros
comme une théorie unique, mais en détails elle aura une diversité
illimitée de variantes possibles (non-équivalentes).
- La théorie des modèles est l'étude des théories (leurs formalismes
comme systèmes de symboles), et des systèmes (modèles possibles des
théories). La théorie de la démonstration complète cela, en décrivant des
formalismes possibles des règles de preuves. La théorie des modèles est généralement
entendue comme un thème général (admettant des variantes de concepts),
mais peut être spécifiée en versions précises, donc des théories mathématiques
appelées cadres logiques, chacune fournissant un
format d’expression précis pour une diversité de théories possibles, et (si complétée par
une théorie de la démonstration) un format dans lequel toutes les preuves de chacune
de ces théories peuvent en principe être exprimées. Il y a un principal cadre logique,
essentiellement unique, appelé logique du premier ordre, par lequel
les concepts de théorie, de théorème (énoncé prouvable) et de cohérence
de chaque théorie, trouvent leurs définitions mathématiques naturelles;
mais d'autres cadres logiques sont parfois nécessaires aussi.
Chacune est le cadre naturel pour formaliser l'autre: toute théorie
des ensembles se formalise comme théorie décrite par la théorie des
modèles; celle-ci vient mieux comme développement de la
théorie des ensembles (définissant théories et systèmes comme
objets complexes), que directement comme théorie. Ces deux
liens doivent être considérés séparément : les deux rôles de la théorie des
ensembles, comme cadre et comme objet d'étude pour la théorie des
modèles, doivent être distingués. Mais ces formalisations
nécessiteront un long travail pour être complétées.
Other languages:
EN : 1. First foundations of
mathematics : 1.1. Introduction
to the foundation of mathematics

