Set Theory and Foundations of Mathematics
1. First foundations of mathematics

Sylvain Poirier
http://settheory.net/

1.1. Introduction to the foundations of mathematics

What is mathematics

Mathematics is the study of systems of elementary objects, whose only considered nature is to be exact, unambiguous (two objects are equal or different, related or not; an operation gives an exact result...). Mathematics as a whole can be seen as «the science of all possible worlds» of this kind (of exact objects).
Mathematical systems are conceived as «existing» independently of our usual world or any particular sensation, but their study requires some form of representation. Diverse ways can be used, that may be equivalent (giving the same results) but with diverse degrees of relevance (efficiency) that may depend on purposes. Ideas may first appear as more or less visual intuitions which may be expressed by drawing or animations, then their articulations may be expressed in words or formulas for careful checking, processing and communication. To be freed from the limits or biases of a specific form of representation, is a matter of developing other forms of representation, and exercizing to translate concepts between them. The mathematical adventure is full of plays of conversions between forms of representation, which may reflect articulations between mathematical systems themselves.

Theories

Mathematics is split into diverse branches according to the kind of systems being considered. These frameworks of any mathematical work may either remain implicit (with fuzzy limits), or formally specified as theories. Each theory is the study of a supposedly fixed system that is its world of objects, called its model. But each model of a theory may be just one of its possible interpretations, among other equally legitimate models. For example, roughly speaking, all sheets of paper are systems of material points, models of the same theory of Euclidean plane geometry, but independent of each other.

The word «theory» may take diverse meanings between uses, from mathematical ones to those of ordinary language and other sciences. Let us first present the distinction by nature (general kind of objects); the other distinction, by intent (realism vs. formalism) is introduced below and in 1.9.

Non-mathematical theories describe roughly or qualitatively some systems or aspects of the world (fields of observation) which escape exact self-sufficient description. For example, usual descriptions of chemistry involve drastic approximations, recollecting some rough accounts of seemingly arbitrary effects and laws, whose deductions from quantum physics are often out of reach of direct calculations. The lack of clear distinction of objects and their properties induces risks of mistakes when approaching them and trying to infer some properties from others, such as to infer some global properties of a system from likely, fuzzy properties of its parts.

Pure mathematical theories, only describing exact systems, can usually be protected from the risk to be «false», by use of rigorous methods (formal rules) designed to ensure preserving the exact conformity of theories to their intended models.

In between both, applied mathematical theories, such as theories of physics are also mathematical theories but the mathematical systems they describe are meant as idealized (simplified) versions of aspects of given real-world systems while neglecting other aspects; depending on its accuracy, this idealization (reduction to mathematics) also allows for correct deductions within accepted margins of error.

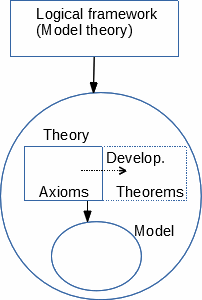Foundations and developments

Any mathematical theory, which describes its model(s), is made of a content and is itself described by a logical framework. The content of a theory is made of components which are pieces of description (concepts and information we shall describe in 1.3). A theory starts with a choice of foundation made of a logical framework and an initial version of its content (hopefully rather small, or at least simply describable). The components of this initial version are qualified as primitive.
The study of the theory progresses by choosing some of its possible developments : new components resulting from its current content (by rules also described by the logical framework), and that can be added to it to form its next content. These different contents, having the same meaning (describing the essentially same models), play the role of "different presentations of the same theory". Any other possible development (not yet chosen) can still be added later, as the part of the foundation that could generate it remains. Thus, the totality of possible developments of a theory, independent of the order chosen to process them, already forms a kind of «reality» that these developments explore.

To express the properties of its models, each theory includes a list of statements, which are formulas meant as true when interpreted in any model. Its primitive statements are called axioms. Further statements called theorems are added by development to the content, under the condition that they are proven (deduced) from previous ones : this ensures them to be true in all models, provided that previous ones were. Theorems can then be used in further developments in the same way as axioms. A theory is consistent if its theorems will never contradict each other. Inconsistent theories cannot have any model, as the same statement cannot be true and false on the same system. The Completeness Theorem (1.9, 1.10, 4.7) will show that the range of all possible theorems precisely fits the more interesting reality of which statements stay true across the range of all models (which indeed exist for any consistent theory).
Other kinds of developments (definitions and constructions) adding other components beyond statements, will be described in 1.5, 1.D, 4.10 and 4.11.

There are possible hierarchies between theories, where some can play a foundational role for others. For instance, the foundations of several theories may have a common part forming a simpler theory, whose developments are applicable to all.
A fundamental work is to develop, from a simple initial basis, a convenient body of knowledge to serve as a more complete "foundation", endowed with efficient tools opening more direct ways to further interesting developments.

Platonism vs Formalism

Mathematics, or each theory, may be approached in two ways (detailed in 1.9): Many philosophers of mathematics carry obsolete conceptions of such views as forming a list of multiple opposite beliefs (candidate truths) on the real nature of mathematics. But after examination, just remain these two necessary and complementary views, with diverse shares of relevance depending on topics.

By its limited abilities, human thought cannot operate in any fully realistic way over infinite systems (or finite ones with unlimited size), but requires some kind of logic for extrapolation, roughly equivalent to formal reasonings developed from some foundations ; this work of formalization can prevent possible errors of intuition. Moreover, mathematical objects cannot form any completed totality, but only a forever temporary, expanding realm, whose precise form is an appearance relative to a choice of formalization.

But beyond its inconvenience for expressing proofs, a purely formalistic view cannot hold either because the clarity and self-sufficiency of any possible foundation (starting position with formal development rules), remain relative: any starting point had to be chosen somehow arbitrarily, taken from and motivated by a larger perspective over mathematical realities; it must be defined in some intuitive, presumably meaningful way, implicitly admitting its own foundation, while any try to specify the latter would lead to a path of endless regression, whose realistic preexistence would need to be admitted.

The cycle of foundations

The general foundation of all mathematics is itself a mathematical study, thus a branch of mathematics, called mathematical logic. Despite the simplicity of nature of mathematical objects, it turns out to be quite complex (though not as bad as a physics theory of everything): by describing the general form of theories and systems they may describe, it forms the general framework of all branches of mathematics... including itself. So providing the foundation of each considered foundation (unlike ordinary mathematical works that go forward from an assumed foundation), it does not form a precise starting point, but a wide loop composed of easier and harder steps. Still this cycle truly plays a foundational role for mathematics, providing to its diverse branches many useful concepts (tools, rigor, inspirations and answers to diverse philosophical questions).
(This is similar to the use of dictionaries defining each word by other words, or to this other science of complex exact systems: computer programming. Indeed computers can be simply used, knowing what you do but not why it works; their working is based on software that was written in some language, then compiled by other software, and on the hardware and processor whose design and production were computer assisted. And this is much better in this way than at the birth of this field.)
It is dominated by two theories:

Each one is the natural framework to formalize the other: each set theory is formalized as a theory described by model theory; the latter better comes as a development from set theory (defining theories and systems as complex objects) than directly as a theory. Both connections must be considered separately: both roles of set theory, as a basis and an object of study for model theory, must be distinguished. But these formalizations will take a long work to complete.

1.2. Variables, sets, functions and operations

Starting mathematics is a matter of introducing some simple concepts from the founding cycle, which may seem as self-sufficient as possible (while they cannot be absolutely so). A usual and natural solution is to start with a set theory not fully formalized as an axiomatic theory. This will be briefly done in 1.2, intuitively explaining the concepts of set and function. Then 1.3 will start introducing model theory, by which any theory including set theory can be formalized, and later sections will explain the main subtleties (paradoxes) in the resulting picture of mathematical foundations.

Constants

A constant symbol is a symbol seen as denoting a unique object, called its value. Examples: 3, ⌀, ℕ. Those of English language usually take the form of proper names and names with «the» (singular without complement).

Free and bound variables

A variable symbol (or a variable), is a symbol which, instead having an a priori definite value, comes with the concept of its possible values, or possible interpretations, each of which give it a particular value. Each possibility gives it a role of constant. There may be any number of these possible values, including infinitely many, only one or even none.
It can be understood as limited by a box, whose inside has multiple versions in parallel, articulating different viewpoints over it: More precisely with respect to given theories, fixing a variable means taking a free variable in a theory and more lengthily ignoring its variability, therefore simulating the use of the other theory obtained by holding this symbol as a constant.
The diverse «internal viewpoints», corresponding to each possible value seen as fixed, may be thought of as abstract «locations» in the mathematical universe, while the succession of views over a symbol (qualifying it as a constant, a free variable or a bound variable), can be seen as a first expression of the flow of time in mathematics: a variable is bound when all the diverse "parallel locations inside the box" (possible values) are past. All these places and times are themselves purely abstract, mathematical entities.

Ranges and sets

The range of a variable, is the meaning it takes when seen as bound: it is the «knowledge» of the considered totality of its possible or authorized values (seen in bulk: unordered, ignoring their context), that are called the elements of this range. This «knowledge» is an abstract entity that, depending on context, may be able to actually process (encompass) infinities of objects (unlike human thought). Any range of a variable is called a set.
A variable has a range when it can be bound, i.e. when an encompassing view over all its possible values is given. Not all variables of set theory will have a range. A variable without a range can still be free, which is no more an intermediate status between fixed and bound, but means it can take some values or some other values with no claim of exhausitivity.

Cantor defined a set as a «gathering M of definite and separate objects of our intuition or our thought (which are called the "elements" of M) into a whole». He explained to Dedekind : «If the totality of elements of a multiplicity can be thought of... as "existing together", so that they can be gathered into "one thing", I call it a consistent multiplicity or a "set".» (We expressed this "multiplicity" as that of values of a variable).
He described the opposite case as an «inconsistent multiplicity» where «admitting a coexistence of all its elements leads to a contradiction». But non-contradiction cannot suffice to generally define sets: the consistency of a statement does not imply its truth (i.e. its negation may be true but unprovable); facts of non-contradiction are often themselves unprovable (incompleteness theorem); and two separately consistent coexistences might contradict each other (Irresistible force paradox / Omnipotence paradox).

A variable is said to range over a set, when it is bound with this set as its range. Any number of variables can be introduced ranging over a given set, independently of each other and of other variables.
Systematically renaming a bound variable in all its box, into another symbol not used in the same context (same box), with the same range, does not change the meaning of the whole. In practice, the same letter can represent several separate bound variables (with separate boxes), that can take different values without conflict, as no two of them are anywhere free together to compare their values. The common language does this continuously, using very few variable symbols («he», «she», «it»...)

Functions

A function is an object f made of the following data: In other words, it is an entity behaving as a variable whose value is determined by that of another variable called its argument with range Dom f : whenever its argument is fixed (gets a name, here "x", and a value in Dom f), f becomes also fixed, written f(x). This amounts to conceiving a variable f where the "possible views" on it as fixed, are treated as objects x conceptually distinct from the resulting values of f. As we shall see later, such an entity (dependent variable) f would not be (viewable as) a definite object of set theory if its argument had no range, i.e. could not be bound (it would only be a meta-object, or object of model theory, that we shall call a functor in 1.4)

Operations

The notion of operation generalizes that of function, by admitting a finite list of arguments (variables with given respective ranges) instead of one. So, an operation gives a result (a value) when all its arguments are fixed. The number n of arguments of an operation is called its arity ; the operation is called n-ary. It is called unary if n=1 (it is a function), binary if n=2, ternary if n=3...
The concept of nullary operation (n=0) is superfluous, as their role is already played by their unique value; 2.3 will show how to construct operations with arity > 1 by means of functions.

Like for functions, the arguments of operations are basically denoted not by symbols but by places around the operation symbol, to be filled by any expression giving them desired values. Diverse display conventions may be used (1.5). For instance, using the left and right spaces in parenthesis after the symbol f, we denote f(x,y) the value of a binary operation f on its fixed arguments named x and y (i.e. its value when its arguments are assigned the fixed values of x and y).

An urelement (pure element) is an object not playing any other role than that of element: it is neither a set nor a function nor an operation.

1.3. Form of theories: notions, objects and meta-objects

The variability of the model

Each theory describes its model as a fixed system. But from the larger viewpoint of model theory, this is a mere «choice» of one possible model (interpretation) in a (usually infinite) range of other existing, equally legitimate models of the same theory. Now this fixation of the model, like the fixation of any variable, is just the simple act of picking any possibility, ignoring any issue of how to specify an example in this range. Actually these «choice» and «existence» of models can be quite abstract. In details, the proof of the Completeness theorem will effectively «specify» a model of any consistent theory for the general case, but this definition will not be very explicit, due to its use of infinity. Regardless this difficulty, the attitude of implicitly fixing a model when formally studying any mathematical theory, remains the normal way of interpreting it (except somehow for set theory as explained in 2.A).

Notions and objects

Each theory has its own list of notions (usually designated by common names), formally serving as the kinds of variables it can use ; each model interprets each notion as a set that is the common range of all variables of this kind. For example, Euclidean geometry has the notions of «point», «straight line», «circle» and more, and is usually expressed using a different style of variable symbol for each. The objects of a theory in a model, are all possible values of its variables of all kinds (the elements of all its notions) in this model.

One-model theory

Any discussion on several theories T and systems M that may be models of those T, takes place in model theory, with its notions of «theory» and «system» that are the respective kinds of the variables T and M. But when focusing on one theory with a fixed model, the variables T and M now fixed disappear from the list of variables. Their kinds, the notions of theory and model, disappear from the notions list too. This reduces the framework, from some model theory, to that of a one-model theory.
A model of a one-model theory, is a system [T,M] which combines a theory T with a model M of T.

The diversity of logical frameworks

The role of a logical framework, as a precise version of (one-)model theory with its proof theory, is to describe : Here are those we shall see, roughly ordered from the poorest to the most expressive (though the order depends on the ways to relate them): We shall first describe the main two of them in parallel. First-order logic is the most common version of model theory, describing first-order theories we shall also call generic theories. Set theory, which can encompass all other theories, can also encompass logical frameworks and thus serve itself as the ultimate logical framework as will be explained in 1.D.
Most frameworks manage notions as types (usually in finite number for each theory) classifying both variables and objects. Notions are called types if each object belongs to only one of them, which is then also called the type of the variables that can name it. For example, an object of Euclidean geometry may be either a point or a straight line, but the same object cannot be both a point and a straight line. But set theory will need more notions beyond types: classes, which will be introduced in 1.7.

Examples of notions from various theories

Theory Kinds of objects (notions)
Generic theories Urelements classified by types to play different roles
Set theory Elements, sets, functions, operations, relations, tuples...
Model theory Theories, systems and their components (listed below)
 One-model theory    Objects, symbols, types or other notions, Booleans,
structures (operators, predicates), expressions (terms, formulas)...
Arithmetic Natural numbers
Linear Algebra Vectors, scalars...
Geometry Points, straight lines, circles...

Meta-objects

The notions of a one-model theory (1MT), normally interpreted in [T,M], classify the components of T («type», «symbol», «formula»...), and those of M («object», and tools to interpret components and expressions of T there). But the same notions (which may belong to another logical framework) can be interpreted in [1MT, [T,M]], by putting the prefix meta- on them.

By its notion of «object», each one-model theory distinguishes the objects of T in M from the rest of its own objects in [T,M], which are the meta-objects. The above rule of use of the meta prefix would let every object be a meta-object; but we will make a vocabulary exception by only calling meta-object those which are not objects: symbols, types or other notions, Booleans, structures, expressions...

Set theory only knows the ranges of some of its own variables, seen as objects (sets). But, seen by one-model theory, every variable of a theory has a range among notions, which are meta-objects only.

Components of theories

In a given logical framework, the content of a theory consists in 3 lists of components of the following kinds, where those of each of the latter two kinds are finite systems using those of the previous kind.

Set-theoretical interpretations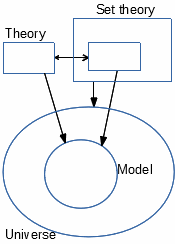

Any generic theory can be interpreted (inserted, translated) in set theory by converting its components into components of set theory. This is the usual view of ordinary mathematics, seeing many systems as «sets with relations or operations such that...», with possible connections between these systems. Let us introduce both the generic interpretations applicable to any generic theory, and other ones usually preferred for some specific theories.

Any interpretation converts each abstract type into a symbol (name) designating a set called interpreted type (serving as the range of variables of that type, whose use is otherwise left intact). This symbol is usually a fixed variable in the generic case, but can be accepted as constant symbol of set theory in special cases such as numbers systems (ℕ, ℝ...).
In generic interpretations, all objects (elements of interpreted types) are urelements, but other kinds of interpretations called standard by convention for specific theories may do otherwise. For example, standard interpretations of geometry represent points by urelements, but represent straight lines by sets of points.

Generic interpretations will also convert structure symbols into fixed variables (while standard ones may define them using the language of set theory). Any choice of fixed values of all types and structure symbols, defines a choice of system. When the language is seen as a set (in particular if it is finite) which is usually the case, models are themselves objects of set theory, owing their multiplicity to the variability of types and structure symbols. This integrates all needed theories into the same set theory, while gathering representatives of all their considered models inside a common model of set theory. This is why models of set theory are called universes.

When adopting set theory as our conceptual framework, this concept of "interpretation" becomes synonymous with the choice (designation) of a model.

1.4. Structures of mathematical systems

The structures, designated in each interpretation by the structure symbols forming a given language, form a described system by relating the objects of the diverse types, giving their roles to the objects of each type with respect to those of other types. Depending on details, the roles so given to objects of some types may be understood as those of complex objects, though all this can work with bare objects like urelements.

First-order structures

The kinds of structures (and thus the kinds of structure symbols) allowed in first-order theories, thus called first-order structures, are split into operators and predicates as described below. More powerful structures called second-order structures will be introduced in 5.1, coming from set theoretical tools or as packs of an additional type with first-order structures.
An operator is an operation between interpreted types. On the side of the theory before interpretation, each operator symbol comes with its symbol type made of In a theory with only one type, this data is reduced to the arity.
The constant symbols (or constants) of a theory are its nullary operator symbols (having no argument).
Unary operators (that are functions) will be called here functors (*).

The list of types is completed by the Boolean type, interpreted as the pair of elements (the set of two elements) we shall denote 1 for «true» and 0 for «false». A variable of this type (outside the theory) is called a Boolean variable.

A para-operator is an operator in the generalized sense allowing the Boolean type among its types of arguments and results.
A (logical) connective is a para-operator with only Boolean arguments and values.
A predicate is a para-operator with Boolean values, and at least one argument but no Boolean argument.

Structures of set theory

Formalizing set theory, means describing it as a theory with its notions, structures and axioms. We shall do this in a dedicated logical framework, different from but convertible into first-order logic by a procedure described in 2.1.
This relates the terminologies of set theory and one-model theory in a different way than when a theory is interpreted in set theory. To keep the natural names of set theoretical notions (sets, functions...) when defined by this formalization, it would become incorrect to still use them in the sense of the previous link (where notions were "sets" and operators were "operations"). To avoid confusion, let us here only use the model theoretical notions as our conceptual framework, ignoring their set theoretical interpretations. Ways to put both links together, and to reconcile both conceptions of the same theories (descriptions by model theory and interpretations in set theory) will be described in 1.7 and 1.D.

Let us admit 3 primitive notions : elements (all objects), sets and functions. Here are their main primitive structures.
One aspect of the role of sets is given by the binary predicate ∈ of belonging or membership : for any element x and any set E, we say that x is in E (or x belongs to E, or x is an element of E, or E contains x) and write x ∈ E, to mean that x is a possible value of the variables with range E.
Functions f play their role by two operators: the domain functor Dom, and the function evaluator, binary operator that is implicit in the notation f(x), with arguments f and x, giving the value of any function f at any element x of Dom f.

More primitive symbols will be presented in 1.7 and 1.8, then most other primitive symbols and axioms will be introduced in 1.A, 2.1, 2.2 and 2.7.

About ZFC set theory

The Zermelo-Fraenkel set theory (ZF, or ZFC with the axiom of choice) is a generic theory with only one type «set», one structure symbol ∈ , and axioms. It implicitly assumes that every object is a set, and thus a set of sets and so on, built over the empty set.
As a rather simply expressible but very powerful set theory for an enlarged founding cycle, it can be a good choice indeed for specialists of mathematical logic to conveniently prove diverse difficult foundational theorems, such as the unprovability of some statements, while giving them a scope that is arguably among the best conceivable ones.
But despite the habit of authors of basic math courses to conceive their presentation of set theory as a popularized or implicit version of ZF(C), it is actually not an ideal reference for a start of mathematics for beginners:

Formalizing types and structures as objects of one-model theory

To formalize one-model theory through the use of the meta- prefix, both meta-notions of "types" and "structures" are given their roles by meta-structures as follows.

Since one-model theory assumes a fixed model, it only needs one meta-type of "types" to play both roles of abstracts types (in the theory) and interpreted types (components of the model), respectively given by two meta-functors: one from variables to types, and one from objects to types. Indeed the more general notion of «set of objects» is not used and can be ignored.

But the meta-notion of structure will have to remain distinct from the language, because more structures beyond those named in the language will be involved (1.5). Structures will get their roles as operations, from meta-structures similar to the function evaluator (see 3.2-3.3 for clues), while the language (set of structure symbols) will be interpreted there by a meta-functor from structure symbols to structures.
However, this mere formalization would leave undetermined the range of this notion of structure. Trying to conceive this range as that of «all operations between interpreted types» would leave unknown the source of knowledge of such a totality. This idea of totality will be formalized in set theory as the powerset (2.7), but its meaning will still depend on the universe where it is interpreted, far from our present concern for one-model theory.

1.5. Expressions and definable structures

Terms and formulas

Given the first two layers of a theory (a list of types and a language), an expression is a finite system of occurrences of symbols, where, intuitively speaking, an occurrence of a symbol in an expression is a place where that symbol is written (more details later).

Each expression comes in the context of a given list of available free variables. Any expression will give (define) a value (either an object or a Boolean) for each possible data of

The type of an expression, determined by its syntax as described below, gives the type of all its possible values. Expressions with Boolean type are called formulas; others, whose type belongs to the given types list (their values will be objects), are called terms.

For example, « x+x » is a term with two occurrences of the variable «x», and one of the addition symbol «+».

The diverse kinds of symbols

In expressions of first-order theories and set theory, symbols of the following kinds may occur. In first-order logic, let us call logical symbols the quantifiers and symbols of para-operators outside the language (equality, connectives and conditional operator): their list and their meaning in each system are determined by the logical framework and the given types list, which is why they are not listed as components of individual theories.

Root and sub-expressions

Each expression contains a special occurrence of a symbol called its root, while each other occurrence of a symbol there, is the root of a unique sub-expression (another expression contained in the given one, and which we may call the sub-expression of that occurrence). The type of an expression is given by the type of result of its root.

Expressions are built successively, in parallel between different lists of available free variables. The first and simplest ones are made of just one symbol (as root, having a value by itself) : constants and variables are the first terms; the Boolean constants 1 and 0 are the simplest formulas.
The next expressions are then successively built as made of the following data:

An algebraic term is a term with only free variables and operator symbols ; these are the only terms in first-order logic without conditional operator. This notion for only one type, will be formalized as a kind of system in set theory in 4.1.

Display conventions

The display of this list of sub-expressions directly attached to the root requires a choice of convention. For a para-operator symbol other than constants : Parenthesis can also be used to distinguish (separate) the subexpressions, thus distinguish the root of each expression from other occurring symbols. For example the root of (x+y)n is the exponentiation operator.

Variable structures

Usually, only few objects are named by the constants in a given language. Any other objects can be named by a fixed variable, whose status depends on the choice of theory to see it: The difference vanishes in generic interpretations which turn constant symbols into variables (whose values define different models).
By similarity to constants which are particular structures (nullary operators), the concept of variable can be generalized to that of variable structure. But those beyond nullary operations (ordinary variables) escape the above list of allowed symbols in expressions. Still some specific kinds of use of variable structure symbols can be justified as abbreviations (indirect descriptions) of the use of legitimate expressions. The main case of this is explained below, forming a development of the theory ; more possible uses will be introduced in 1.10 (the view of a use as an abbreviation of other works amounts to using a developed version of the logical framework).

Structures defined by expressions

In any theory, one can legitimately introduce a symbol meant either as a variable structure (operator or predicate) or a Boolean variable (nullary predicate, not a "structure"), as abbreviation of, thus defined by, the following data : The variability of this structure is the abbreviation of the variability of all its parameters.

In set theory, any function f is synonymous with the functor defined by the term f(x) with argument x and parameter f (but the domain of this functor is Dom f instead of a type).
The terms without argument define simple objects (nullary operators) ; the one made of a variable of a given type, seen as parameter, suffices to give all objects of its type.

Now let us declare the meta-notion of "structure" in one-model theory, and thus those of "operator" and "predicate", as having to include at least all those reachable in this way: defined by any expression with any possible values of parameters. The minimal version of such a meta-notion can be formalized as a role given to the range of all combinations of an expression with fixed values of its parameters. As this involves the infinite set of all expressions, this meta-notion usually escapes (is inaccessible by) the described theory itself : no fixed expression can suffice to simulate it. Still when interpreting this in set theory, more operations between interpreted types (undefinable ones) usually exist in the universe. Among the few exceptions, the full set theoretical range of a variable structure with all arguments ranging over finite sets (as interpreted types) with given size limits, can be reached by one expression whose size depends on these limits.

Invariant structures

An invariant structure of a given system (interpreted language), is a structure defined from its language without parameters (thus a constant one). This distinction of invariant structures from other structures, generalizes the distinction between constants and variables, both to cases of nonzero arity, and to what can be defined by expressions instead of directly named in the language.

Indeed any structure named by a symbol in the language is directly defined by it without parameter, and thus invariant. As will be further discussed in 4.10, theories can be developed by definitions, which consists in naming another invariant structure by a new symbol added to the language. Among aspects of the preserved meaning of the theory, are the meta-notions of structure, invariant structure, and the range of theorems expressible with the previous language.

1.6. Logical connectives

We defined earlier the concept of logical connective. Let us now list the main useful ones, beyond both nullary ones (Boolean constants) 1 and 0. (To this will be added the conditional connective in 2.4).

Tautologies

Their properties will be expressed by tautologies, which are formulas only involving connectives and Boolean variables (here written A, B, C), and true for all possible combinations of values of these variables. So, they also give necessarily true formulas when replacing these variables by any defining formulas using any language and interpreted in any systems. Such definitions of Boolean variables by formulas of a theory may restrict their ranges of possible values depending on each other.

Tautologies form the rules of Boolean algebra, an algebraic theory describing operations on the Boolean type, itself naturally interpreted as the pair of elements 0 and 1 (but also admitting more sophisticated interpretations beyond the scope of this chapter).

The binary connective of equality between Booleans is written ⇔ and called equivalence: A ⇔ B is read «A is equivalent to B».

Negation

The only useful unary connective is the negation ¬, that exchanges Booleans (¬A is read «not A»):
¬1
¬0
¬(¬A) 		⇔ 0
⇔ 1
⇔ A
It is often denoted by barring the root of its argument, forming with it another symbol with the same format:
x ≠ y
x ∉ E
(A ⇎ B)
 ⇔ ¬(x = y)
⇔ ¬(x ∈ E)
⇔ (A ⇔ ¬B)
 (x is not equal to y)
(x is not an element of E)
(inequivalence)

Conjunctions, disjunctions

The conjunction ∧ means «and», being true only when both arguments are true;
The disjunction ∨ means «or», being true except when both arguments are false.
Each of them is :
Idempotent
(A ∧ A) ⇔ A
(A ∨ A) ⇔ A
 Commutative
(B∧A) ⇔ (A∧B)
(B∨A) ⇔ (A∨B)
Associative
((A∧B)∧C) ⇔ (A∧(B∧C))
((A∨B)∨C) ⇔ (A∨(B∨C))
 Distributive over the other
(A ∧ (B∨C)) ⇔ ((A∧B) ∨ (A∧C))
(A ∨ (B∧C)) ⇔ ((A∨B) ∧ (A∨C))

This similarity (symmetry) of their properties comes from the fact they are exchanged by negation:

(A ∨ B) ⇎ (¬A ∧ ¬B)
(A ∧ B) ⇎ (¬A ∨ ¬B)

The inequivalence is also called exclusive or because (A ⇎ B) ⇔ ((A ∨ B) ∧ ¬(A ∧ B)).

Chains of conjunctions such as (A ∧ B ∧ C), abbreviate any formula with more parenthesis such as ((A ∧ B) ∧ C), all equivalent by associativity ; similarly for chains of disjunctions such as (A ∨ B ∨ C).

Asserting (declaring as true) a conjunction of formulas amounts to successively asserting all these formulas.

Implication

The binary connective of implication ⇒ is defined as (A ⇒ B) ⇔ ((¬A) ∨ B). It can be read «A implies B», «A is a sufficient condition for B», or «B is a necessary condition for A». Being true except when A is true and B is false, it expresses the truth of B when A is true, but no more gives information on B when A is false (as it is then true).
Moreover,
(A ⇒ B) ⇎
(A ⇒ B) ⇔		 (A ∧ ¬B)
(¬B ⇒ ¬A)
The formula ¬B ⇒ ¬A is called the contrapositive of A ⇒ B.
The equivalence can also be redefined as
(A ⇔ B) ⇔ ((A ⇒ B) ∧ (B ⇒ A)).
Thus in a given theory, a proof of A ⇔ B can be formed of a proof of the first implication (A ⇒ B), then a proof of the second one (B ⇒ A), called the converse of (A ⇒ B).

The formula A ∧ (A ⇒ B) is equivalent to A ∧ B but will be written A ∴ B, which reads «A therefore B», to indicate that it is deduced from the truths of A and A ⇒ B.

Negations turn the associativity and distributivity of ∧ and ∨, into various tautologies involving implications:

(A ⇒ (B ⇒ C)) ⇔ ((A ∧ B) ⇒ C)
(A ⇒ (B ∨ C)) ⇔ ((A ⇒ B) ∨ C)

(A ⇒ (B ∧ C)) ⇔ ((A ⇒ B) ∧ (A ⇒ C))
((A ∨ B) ⇒ C) ⇔ ((A ⇒ C) ∧ (B ⇒ C))
((A ⇒ B) ⇒ C) ⇔ ((A ∨ C) ∧ (B ⇒ C))
(A ∧ (B ⇒ C)) ⇔ ((A ⇒ B) ⇒ (A ∧ C))
Finally,
(A ⇒ B) ⇒ ((A∧C) ⇒ (B∧C))
(A ⇒ B) ⇒ ((A∨C) ⇒ (B∨C)).

Chains of implications and equivalences

In a different kind of abbreviation, any chain of formulas linked by ⇔ and/or ⇒ will mean the chain of conjunctions of these implications or equivalences between adjacent formulas:

(A ⇒ B ⇒ C) ⇔ ((A ⇒ B) ∧ (B ⇒ C)) ⇒ (A ⇒ C)
(A ⇔ B ⇔ C) ⇔ ((A ⇔ B) ∧ (B ⇔ C)) ⇒ (A ⇔ C)
0 ⇒ A ⇒ A ⇒ 1
(¬A) ⇔ (A ⇒ 0) ⇔ (A ⇔ 0)
(A ∧ 1) ⇔ A ⇔ (A ∨ 0) ⇔ (1 ⇒ A) ⇔ (A ⇔ 1)
(A ∧ B) ⇒ A ⇒ (A ∨ B)

1.7. Classes in set theory

In any system, a class is a unary predicate A seen as the set of objects where A is true, that is «the class of all x such that A(x)».
In a set theoretical universe, each set E is synonymous with the class of the x such that x∈E (defined by the formula x∈E with argument x and parameter E). However, this involves two different interpretations of the notion of set, that need to be distinguished as follows.

Standard universes and meta-sets

Interpreting (inserting) set theory into itself, involves articulating two interpretations (models) of set theory, which will be distinguished by giving the meta- prefix to the one used as framework. Aside generic interpretations, set theory has a standard kind of interpretations into itself, where each set is interpreted by the class (meta-set) of its elements (the synonymous set and meta-set, i.e. with the same elements, are now equal), and each function is interpreted by its synonymous meta-function.
This way, any set will be a class, while any class is a meta-set of objects. But some meta-sets of objects are not classes (no formula with parameters can define them ; giving examples would be paradoxical as it would mean defining something undefinable, yet 1.B introduces such possibilities); and some classes are not sets, such as the class of all sets (see Russell's paradox in 1.8), and the universe (class of all objects, defined by 1).

Definiteness classes

Set theory accepts all objects as «elements» that can belong to sets and be operated by functions (to avoid endless further divisions between sets of elements, sets of sets, sets of functions, mixed sets...). This might be formalized keeping 3 types (elements, sets and functions), where each set would have a copy as element, identified by a functor from sets to elements, and the same for functions. But beyond these types, our set theory will anyway need more notions as domains of its structures, which can only be conveniently formalized as classes. So, let us keep "element" as the only type containing all objects, and formalize the notions of set and function as classes named by predicate symbols:

Set = «is a set»
Fnc = «is a function»

In first-order logic, any expression is ensured to take a definite value, for every data of a model and values of all free variables there (by virtue of its syntactic correction, that is implicit in the concept of «expression»). But in set theory, this may still depend on the values of free variables.
So, an expression A (and any structure defined from it) will be called definite, if it actually takes a value for the given values of its free variables (seen as arguments and parameters of any structure it defines). This condition is itself an everywhere definite predicate, expressed by a formula dA with the same free variables. Choosing one of these as argument, the class it defines is the meta-domain, called class of definiteness, of the unary structure defined by A.
Expressions should be only used where they are definite, which will be done rather naturally. The definiteness condition of (x ∈ E) is Set(E). That of the function evaluator f(x) is Fnc(f) ∧ x ∈ Dom f.
But the definiteness of the last formula needs a justification, given below.

Extended definiteness

A theory with partially definite structures, like set theory, can be formalized (translated) as a theory with one type and everywhere definite structures, keeping intact all expressions and their values wherever they are definite : models are translated one way by giving arbitrary values to indefinite structures (e.g. a constant value), and in the way back by ignoring those values. Thus, an expression with an indefinite subexpression may be declared definite if its final value does not depend on these extra values.
In particular for any formulas A and B, we shall regard the formulas A ∧ B and A ⇒ B as definite if A is false, with respective values 0 and 1, even if B is not definite. So, let us give them the same definiteness condition dA ∧ (A ⇒ dB) (breaking, for A ∧ B, the symmetry between A and B, that needs not be restored). This formula is made definite by the same rule provided that dA and dB were definite. This way, both formulas

A ∧ (B ∧ C)
(A ∧ B) ∧ C

have the same definiteness condition (dA ∧ (A ⇒ (dB ∧ (B ⇒ dC)))).

Classes will be defined by everywhere definite predicates, easily expressible by the above rule as follows.
Any predicate A can be extended beyond its domain of definiteness, in the form dA ∧ A (giving 0), or dA ⇒ A (giving 1).
For any class A and any unary predicate B definite in all A, the class defined by A∧B is called the subclass of A defined by B.

1.8. Binders in set theory

The syntax of binders

This last kind of symbol can form an expression by taking a variable symbol, say here x, and an expression F which may use x as a free variable (in addition to the free variables that are available outside), to give a value depending on the unary structure defined by F with argument x. Thus, it separates the «inside» subexpression F having x among its free variables, from the «outside» where x is bound. But in most cases (in most theories...), binders cannot keep the full information on this unary structure, which is too complex to be recorded as an object as we shall see below.

We shall first review both main binders of set theory : the set-builder and the function definer. Then 1.10 will present both main quantifiers. Finally 2.1 and 2.2 will give axioms to complete this formalization of the notions of sets and functions in set theory.

The syntax differs between first-order logic and set theory, which manage the ranges of variables differently. In first-order logic, ranges are types, implicit data of quantifiers. But the ranges of binders of set theory are sets which, as objects, are designated by an additional argument of the binder (a space for a term not using the variable being bound).

Set-builder

For any unary predicate A definite on all elements of a set E, the subclass of E defined by A is a set : it is the range of a variable x introduced as ranging over E, so that it can be bound, from which we select the values satisfying A(x). It is thus a subset of E, written {x∈E | A(x)} (set of all x in E such that A(x)): for all y,

y ∈ {x∈E | A(x)} ⇔ (y ∈ E ∧ A(y))

This combination of characters { ∈ | } forms the notation of a binder named the set-builder: {x∈E | A(x)} binds x with range E on the formula A.

Russell's paradox

If the universe (class of all elements) was a set then, using it, the set builder could turn all other classes, such as the class of all sets, into sets. But this is impossible as can be proven using the set-builder itself :

Theorem. For any set E there is a set F such that F ∉ E. So, no set E can contains all sets.

Proof. F = {x∈E | Set(x) ∧ x ∉ x} ⇒ (F ∈ F ⇔ (F ∈ E ∧ F ∉ F)) ⇒ (F ∉ F ∧ F ∉ E). ∎

This will oblige us to keep the distinctions between sets and classes.

The function definer

The function definer ( ∋ ↦ ) binds a variable on a term, following the syntax E ∋ x ↦ t(x), where Being definite if t(x) is definite for all x in E, it takes then the functor t and restricts its domain (definiteness class) to the set E, to give a function with domain E. So it converts functors into functions, reversing the action of the function evaluator (with the Dom functor) that converted (interpreted) functions into their role (meaning) as functors whose definiteness classes were sets.
The shorter notation x ↦ t(x) may be used when E is determined by the context, or in a meta description to designate a functor by specifying the argument x of its defining term.

Relations

A relation is a role playing object of set theory similar to an operation but with Boolean values : it acts as a predicate whose definiteness classes (ranges of arguments) are sets (so, predicates could be described as relations between interpreted types).

Now unary relations (functions with Boolean values), will be represented as subsets S of their domain E, using the set-builder in the role of definer, and ∈ in the role of evaluator interpreting S as the predicate x ↦ (x ∈ S). This role of S still differs from the intended unary relation, as it ignores its domain E but is definite in the whole universe, giving 0 outside E. This lack of operator Dom does not matter, as E is usually known from the context (as an available variable).

As the function definer (resp. the set-builder) records the whole structure defined by the given expression on the given set, it suffices to define any other binder of set theory on the same expression with the same domain, as made of a unary structure applied to its result (that is a function, resp. a set).

1.9. Axioms and proofs

Statements

An expression is ground if its list of available free variables is empty (all its variables are bound), so that its value only depends on the system where it is interpreted.
In first-order logic, a statement is a ground formula. Thus, a statement A will have a definite Boolean value only depending on the choice of a system M that interprets its language. We denote M⊨A the truth of A in M.
The axioms list of a theory is a set of statements, meant to be all true in some given system(s) called models of the theory. Let us explain.

Realistic vs. axiomatic theories in mathematics and other sciences

Apart from the distinction of nature (mathematical vs. non-mathematical), theories may also differ by the intention of their use, between realism and formalism.

An axiomatic theory is a formally given theory T = (τ, L, X) with an axioms list X, that means to define the class of its models, as that of all systems M interpreting the language L where all axioms (elements of X) are true, which will be denoted M⊨T.

A realistic theory is a theory involved to describe either a fixed or a variable system, i.e. a class of systems, seen as given from some independent reality. Its given axioms are statements which, for some reason, are considered known as true on all these systems. Such a theory is true if all its axioms are indeed true there. In this case, these systems are models, qualified as standard for contrast with other (unintended) models of that theory taken axiomatically.

This truth will usually be ensured for realistic theories of pure mathematics : arithmetic and set theory (though the realistic meaning of set theory will not always be clear depending on considered axioms). These theories will also admit non-standard models, making their realistic and axiomatic meanings effectively differ.
Outside pure mathematics, the truth of realistic theories may be dubious (questionable): non-mathematical statements over non-mathematical systems may be ambiguous (ill-defined), while the truth of theories of applied mathematics may be approximative, or speculative as the intended "real" systems may be unknown (contingent among other possible ones). There, a theory is called falsifiable if, in principle, the case of its falsity can be discovered by comparing its predictions (theorems) with observations. For example, biology is relative to a huge number of random choices silently accumulated by Nature on Earth during billions of years ; it has lots of "axioms" which are falsifiable and require a lot of empirical testing.
Non-realistic theories outside mathematics (not called "axiomatic" by lack of mathematical precision) would be works of fiction describing imaginary or possible future systems.

Euclidean geometry was first conceived as a realistic theory of applied mathematics (for its role of first theory of physics), then became understood as an axiomatic theory of pure mathematics among diverse other, equally legitimate geometries in a mathematical sense; while the real physical space is more accurately described by the non-Euclidean geometry of General Relativity.

Provability

A proof of a statement A in a theory T, is a finite model of a one-proof theory (reduction of proof theory to the description of a single proof), having A as "conclusion" and involving a finite list of axioms among those of T.
Suitable full formalizations of the concept of proof for first-order logic could be found by specialists. Those can take the form of formalized (one-)proof theories (as axiomatic theories), or proof verification algorithms (only requiring an amount of computing resources related to the size of a given proof).
But most mathematical works are only partially formalized : semi-formal proofs are used with just enough rigor to give the feeling that a full formalization is possible, without actually writing it ; an intuitive vision of a problem may seem clearer than a formal reasoning. Likewise, this work will present proofs naturally without explicit full formalization : sometimes using natural language articulations, proofs will mainly be written as successions of statements each visibly true thanks to previous ones, premises, axioms, known theorems and rules of proof, especially those of quantifiers (1.10). End of proof is marked by "∎".
Yet without giving details of any proof theory, let us review some general properties.

We say that A is provable in T, or a theorem of T, and write T ⊢ A if a proof of A in T exists. In practice, we only qualify as theorems the statements known as such, i.e. for which a proof is known. But synonyms for "theorem" are traditionally used according to their importance: a theorem is more important than a proposition; either of them may be deduced from an otherwise less important lemma, and easily implies an also less important corollary.

Any good proof theory needs of course to be sound, which means only "proving" always true statements : provability implies truth in every model (where all axioms are true).

Logical validity

For a given language L, a statement A is called logically valid if it is provable with L, without using any axiom. This might be written ⊢ A but for full accuracy it needs to be written L ⊢ A (meaning that A is theorem of the theory made of L without axiom, thus of any other theory containing L). Then A is true in every system interpreting L, thanks to the soundness of the logical framework.
The simplest logically valid statements are the tautologies (whose Boolean variables are replaced by statements); others will be given in 1.10.

A proof of A using some axioms can also be seen as a proof of (conjunction of these axioms ⇒ A) without axiom, thus making this implication logically valid.

Refutability and consistency

A refutation of A in T, is a proof of ¬A. If one exists (T ⊢ ¬A), the statement A is called refutable (in T).
A statement is called decidable (in T) if it is provable or refutable.
A contradiction of a theory T is a proof of 0 in T. If one exists (T ⊢ 0), the theory T is called contradictory or inconsistent ; otherwise it is called consistent.
A refutation of A in T amounts to a contradiction of the theory T∧A obtained by adding A to the axioms of T.
If a statement is both provable and refutable in T then all are, because it means that T is inconsistent, independently of the chosen statement:

⊢ (A ∧ ¬A) ⇔ 0
((T ⊢ A) ∧ (T ⊢ B)) ⇔ (T ⊢ A∧B)
((T ⊢ A) ∧ (T ⊢ ¬A)) ⇔ (T ⊢ 0).

So a contradiction can be presented as a proof of A with a refutation of A. In an inconsistent theory, every statement is provable. Its framework being sound, such a theory has no model.

Beyond the required quality of soundness of the proof theoretical part of a logical framework, more remarkable is its converse quality of completeness : that for any axiomatic theory it describes, any statement that is true in all models is provable. In other words, any unprovable statement is false somewhere, and any irrefutable statement is true somewhere. Thus, any consistent theory has existing models, but often a diversity of them, as any undecidable statement is true in some and false in others. Adding some chosen undecidable statements to axioms leads to different consistent theories which can «disagree» without conflict, all truly describing different existing systems. This resolves much of a priori divergence between Platonism and formalism while giving proper mathematical definiteness to the a priori intuitive concepts of "proof", "theorem" and "consistency".

1.10. Quantifiers

A quantifier is a binder taking a unary predicate (formula) and giving a Boolean value.

Bounded vs open quantifiers

A quantifier Q is called bounded when following the use format for binders in set theory (1.8) : its range is a set given as an argument. For quantifiers this format is written (Q ∈ , ) filled as (Qx∈E, A(x)) to take as input a unary predicate A, by binding a variable x with range E on any formula here abbreviated as A(x) to mean it defines A with argument x and possible parameters.
Primitively in first-order logic, the ranges of quantifiers are types (the same type as the bound variable, not formally an argument). Any range E (type, class or set) may be marked as an index (QEx, A(x)), or deleted altogether (Qx, A(x)) when it is unimportant or implicit as fixed by the context.
When set theory is formalized in first-order logic, the quantifiers from first-order logic, ranging over the universe, and their variants ranging over classes (defined from them below), are called open quantifiers to be distinguished from the restricted case of bounded quantifiers (as sets are there particular cases of classes). In this context, a formula is qualified as bounded if all its quantifiers are bounded. Only these formulas will be accepted for some uses (1.A, 1.C, 2.1, 2.2).

Both main quantifiers

There are two main quantifiers (from which others will be defined in 2.4): The bounded universal quantifier is definable from the set builder:

(∀x∈E, A(x)) ⇔ {x∈E | A(x)} = E.

Quantifiers with any range can be defined in interpretations, seeing A as a function and its Boolean values as objects:

(∀x, A(x)) ⇔ A = (x ↦ 1)
(∃x, A(x)) ⇔ A ≠ (x ↦ 0)
(∃x, A(x)) ⇎ (∀x, ¬A(x))

(∀x, 1) is always true. Quantifiers over classes can be defined as

(∀C x, A(x)) ⇔ (∀x, C(x) ⇒ A(x))
(∃C x, A(x)) ⇔ (∃x, C(x) ∧ A(x)) ⇔ ∃C∧A x, 1

Inversely any class is definable from a quantifier over it : ∀x, (C(x) ⇔ ∃C y, x=y).

Inclusion between classes

A class A is said to be included in a class B when ∀x, A(x) ⇒ B(x). Then A is a subclass of B, as ∀x, A(x) ⇔ (B(x) ∧ A(x)). Conversely, any subclass of B is included in B.
The inclusion of A in B implies for any predicate C (in cases of definiteness):

(∀B x, C(x)) ⇒ (∀A x, C(x))
(∃A x, C(x)) ⇒ (∃B x, C(x))
(∃C x, A(x)) ⇒ (∃C x, B(x))
(∀C x, A(x)) ⇒ (∀C x, B(x))

Rules of proofs for quantifiers on a unary predicate

Just like expressions were described by allowing to take already made expressions to form new ones, the concept of proof may be formalized by using already known proofs to form new ones. Here are some intuitively introduced rules, still without claim of full formalization.

Existential Introduction. If we have terms t, t′,… and a proof of (A(t) ∨ A(t′) ∨ …), then ∃x, A(x).

Existential Elimination. If ∃x, A(x), then we can introduce a new free variable z with the hypothesis A(z) (the consequences will be true without restricting the generality).

These rules express the meaning of ∃ : going from some term to ∃ then from ∃ to z, amounts to letting z represent that term (without knowing which, but they can be gathered into one by the conditional operator). They give the same meaning to ∃C as to its 2 above equivalent formulas, bypassing (making implicit) the extended definiteness rule for (C ∧ A) by focusing on the case when C(x) is true and thus A(x) is definite.

While ∃ appeared as the designation of an object, ∀ appears as a deduction rule: ∀C x, A(x) means that its negation ∃C x, ¬A(x) leads to a contradiction.

Universal Introduction. If from the mere hypothesis C(x) on a new free variable x we could deduce A(x), then ∀C x, A(x).

Universal Elimination. If ∀C x, A(x) and t is a term satisfying C(t), then A(t).

Introducing then eliminating ∀ is like replacing x by t in the initial proof.

Some logically valid formulas

The above rules can be used to justify the following logically valid formulas

((∀C x, A(x)) ∧ (∀C x, A(x) ⇒ B(x))) ⇒ (∀C x, B(x))
((∃C x, A(x)) ∧ (∀C x, A(x) ⇒ B(x))) ⇒ (∃C x, B(x))
((∀C x, A(x)) ∧ (∃C x, B(x))) ⇒ (∃C x, A(x) ∧ B(x))
(∀C x, A(x)∨B(x)) ⇒ ((∀C x, A(x)) ∨ (∃C x, B(x)))
(∀A x, ∀B y, R(x,y)) ⇔ (∀B y, ∀A x, R(x,y))
(∃A x, ∃B y, R(x,y)) ⇔ (∃B y, ∃A x, R(x,y))
(∃A x, ∀B y, R(x,y)) ⇒ (∀B y, ∃A x, R(x,y))
∀x, (∀y, R(x,y)) ⇒ R(x,x) ⇒ (∃y, R(x,y))

We shall use the following abbreviations, also similarly with bounded quantifiers: Logical validity depends on language because, with only one type

(L ⊢ ∃x, 1) ⇔ (a constant symbol exists in L)

(With more types the condition is more complicated; but as most useful theories require all types to be nonempty, the dependence on language may be ignored in practice)

Completeness of first-order logic

First-order logic was found complete as expressed by the completeness theorem, which was originally Gödel's thesis : from a suitably formalized concept of «proof», the resulting class of (potential) theorems A of any first-order theory T was found to be the "perfect" one, coinciding with the class of universally true statements (true in all models M):

∀A, (T ⊢ A) ⇔ (∀M, (M⊨T)⇒(M⊨A))

Such a proof theory for first-order logic is essentially unique: the equivalence between any two sound and complete proof theories as concerns the existence of a proof of a statement in a theory, concretely appears by the possibility to translate any "proof" for the one into a "proof" for the other.

This quality of first-order logic confirms its central importance in the foundations of mathematics, after its ability to express all mathematics : any logical framework can anyway be developed from set theory (and more directly, any theory from any framework can be somehow interpreted in set theory), itself expressible as a first-order theory.

The proof of the completeness theorem, which requires the axiom of infinity (existence of ℕ) will consist in building a model of any consistent first-order axiomatic theory, as follows (details in 4.6). The (infinite) set of all ground terms with operator symbols derived from the theory (those of its language plus others coming from its existence axioms), is turned into a model by progressively defining each predicate symbol over each combination of values of its arguments there, by a rule designed to keep consistency.

This construction is non-algorithmic : it is made of an infinity of steps, where each step may involve an infinite knowledge (of whether the given predicate on given arguments, seen as a candidate additional axiom, preserves consistency with previously accepted ones). Actually, most foundational theories such as set theories, do not have any algorithmically definable model.

1.11. Second-order universal quantifiers

First-order logic can be developed to allow the use of variable structure symbols as abbreviations of fixed expressions defining these structures with variable parameters, but this way can only bind them on some restricted ranges depending on the chosen expressions (more comments in 1.D).
Now let us call second-order quantifier, a quantifier binding a variable structure symbol over the range of all structures of its symbol type. This may either be conceived as the range of all definable ones (by any expressions with any number of parameters) or as the full set of all such operations (relating the given interpreted types), which exist... in the universe. Using second-order quantifiers means working in some wider logical framework such as some version of second-order logic (described in part 5), depending on details.

As we shall do for the axioms of equality (below) and for set theory (in 2.1 and 2.2), a theory may be first expressed in second-order logic for intuitive reasons, before formally interpreting this as a convenient meta level tool to abbreviate a first-order formalization, as follows.

Let T be a first-order theory, T' its extension by a structure symbol s (without further axiom) and F a statement of T' (in first-order logic) also denoted F(s) when seen as a formula of T using the variable structure symbol s in second-order logic.

Second-order Universal Introduction. If T'⊢F then T entails the second-order statement (∀s, F(s)).

This holds for any model and the full set theoretical range of s, independently of the universe in which models and structures s are searched for.

Second-order Universal Elimination. Once a second-order statement (∀s, F(s)) is accepted in a theory T, it is manifested in first-order logic as a schema of statements, that is an infinite list of statements of the form (∀parameters, F(s)) for each possible replacement of s by a defining expression with parameters.

Applying second-order universal elimination after second-order universal introduction, means deducing from T a schema of theorems, each one deducible in first-order logic by replacing s by its respective definition in the original proof.

Incompleteness of second-order logic

The above rules of proof, which will suffice for our needs, are clearly sound, but unlike first-order logic, second-order logic does not admit any sound and complete proof theory. In the above, the only complete rule of proof is that second-order universal elimination completely formalizes the consequences of ∀ meant as ranging over definable structures. No rule can exhaust the consequences of applying ∀ to the range of "all structures" (including undefinable ones) for the following reason whose details will be developed later.

A theory is called complete if it essentially determines its model. The exact definition is that all models are isomorphic to each other (3.3); but let us understand now that it both determines all properties of its model (values of first-order statements) and excludes non-standard models.
Arithmetic (the theory describing the system ℕ of natural numbers with four symbols 0, 1, +, ⋅ ) can be formalized as a complete theory in second-order logic (axioms listed in 4.3 and 4.4). The only component of this formalization beyond first-order logic is the axiom of induction, using a ∀ ranging over "all unary predicates" (including undefinable ones). However the incompleteness theorem (1.C) will refute the possibility for any algorithm to give the correct values of all first-order statements of arithmetic.

But the range of the mere definable structures of a type cannot be completely defined either for the same reason, since defining the exact infinite range of all possible defining expressions, amounts to defining ℕ.

Axioms of equality

In first-order logic with given types and a given language, some statements involving = are valid (always true) for the range of interpretations keeping = as the = predicate of set theory, but no more for the larger range of interpretations letting it become any other predicate. A possible list of axioms of equality, is a list of some of such statements which suffice to imply all others in this context.
One such list consists in the following 2 axioms per type, where the latter is meant as an axiom schema by second-order universal elimination of the variable unary predicate A:
  1. ∀x, x = x (reflexivity)
  2. ∀A,∀x,y, (x = y ∧ A(y)) ⇒ A(x).
Variables x and y can also serve among parameters in definitions of A. This can be understood by re-ordering quantifiers as (∀x,y, ∀A), or as deduced from the use with an A with parameters a, b, by adapting a logically valid statement from 1.10 :

∀a,b, (∀x,y, R(a, b, x,y)) ⇒ R(a, b, a,b)

Diverse definitions of A give diverse statements (assuming reflexivity):

Statement
3. ∀x,y, x = y ⇒ y = x
4. ∀x,y,z, (x = y ∧ y = z) ⇒ x = z
5. ∀f, ∀x,y, x = y ⇒ f(x) = f(y)
6. ∀A, ∀x,y, x = y ⇒ (A(x) ⇔ A(y))
7. ∀x,y,z, (x = y ∧ z = y) ⇒ z = x		 Quality of =
Symmetric
Transitive


Left Euclidean 		A(u) used
y = u
u = z
f(u) = f(y)
¬A(u)
z = u

5. is a schema of statements with f ranging among functors between any two types.
6. can also be deduced from symmetry.

Remark. (1.∧7.) ⇒ 3., then 3. ⇒ (4. ⇔ 7) so that (1.∧7.) ⇔ (1.∧3.∧4.).
We shall abbreviate (x = y ∧ y = z) as x = y = z.

Another possible list of axioms of equality consists in statements 1. to 5. where f and A range over the mere symbols of the language, each taken once per argument : the full scheme of 2. is implied by successive deductions for each occurrence of symbol in A. This will be further justified in 2.9 (equivalence relations).

Defining new binders

A new free variable symbol x defined by a given term t can be introduced, either declared as a separate line of proof (x = t) serving as axiom, or inside a line as (x = t ∴ ...). This can be justified by the rules as

(∀x, x = x) ∴ t = t ∴ ∃x, (x = t ∴ ...).

Binding one parameter, the definition of a functor symbol f by a term here abbreviated t with variable x (which will justify this abbreviated notation t like a functor symbol), is declared by the axiom

∀x, f(x) = t(x).

Similarly, operator symbols can be defined by binding multiple parameters, and classes and other predicates can be defined in the same way replacing = by ⇔.
Finally, new binders B to be used in a first-order theory T (namely in set theory formalized with its translation as a first-order theory) can be defined by any expression here abbreviated as F(A) as it involves, beyond the language of T, a symbol A of variable unary structure (whose argument will be bound by B). Such a definition can be declared by this second-order axiom :

∀A, (Bx, A(x)) = F(A)

where = becomes ⇔ if values are Boolean. By second-order universal elimination, this comes down to a schema of definitions in first-order logic : for each defining expression for A, the expression (Bx, A(x)) is defined like a structure symbol, by the expression defining F(A), obtained by replacing A by its defining expression inside the expression F. So its available free variables are the parameters of F plus those of A.

Philosophical aspects of the foundations of mathematics

Let us complete our initiation to the foundations of mathematics by more philosophical aspects : how, independently of our time, the mathematical realm is structured by a growing block flow of its own time. First 1.A to 1.C will explain this as affecting model theory, then its role in set theory will be further explored in 1.D and complements to part 2 (clarifying the difference between sets and classes).

1.A. Time in model theory

The time order between interpretations of expressions

The interpretations of expressions of a theory T in a model M depend on each other, thus come as calculated after each other. This time order follows the construction order from sub-expressions to expressions containing them.
For example, to make sense of the formula xy+x=3, the free variables x and y must take values first; then, xy takes a value, obtained by multiplying them. From this, xy+x takes a value, and then the whole formula (xy+x=3) takes a Boolean value, depending on the values of x and y. Finally, taking for example the ground formula ∀x, ∃y, xy+x=3, its Boolean value (which is false in the world of real numbers), «is calculated from» those taken by the previous formula for all possible values of x and y, and therefore comes after them.

The interpretations of a finite list of expressions may be gathered by a single other expression, taking them as sub-expressions. This big expression is interpreted after them all, but still belongs to the same theory.
Now for a single expression to handle an infinite set of expressions (such as the range of all expressions of T, or just all terms or all statements), these expressions must be treated as objects (values of a variable). If T is a foundational theory, it can define (or construct) a system looking like this, so that, in any standard model of T (in a sense we shall specify later), this definition will designate an exact copy of this set of expressions.

However, the systematic interpretation of all expressions of T in M cannot fit any definition by a single expression of T interpreted in the same M. Namely, this forms a part of the combined system [T,M] beyond M, to be described by a one-model theory (1MT) which, even if it can be developed from T, anyway requires another interpretation, at a meta level over M.

The infinite time between models

Without trying to formalize the model theory MT of first-order logic (which will be approached in the next sections) let us sketch a classification of its components (mixing notions, structures and axioms) into parts according to what they describe. Most issues are unchanged by restricting consideration to an 1MT, with model a single system [T,M] of a theory T with a model M, when these T and M (specified by additional axioms of 1MT) are big enough to roughly contain any theory and any system. But some issues may even be unchanged with simpler choices of T and M. This last part describes a part of [T,M] which is determined by the combination of both systems T and M but not directly contained in them : it is built after them.

The metaphor of the usual time

I can speak of «what I meant at that time»: it has a sense if that past saying had one, as I got that meaning and I remember it. But mentioning «what I mean» in isolation, would not itself inform on what it is, as it might be anything, and becomes absurd in a phrase that modifies or contradicts this meaning («the opposite of what I mean»). Mentioning «what I will tell tomorrow», even if I already knew what I will say, would not suffice to already provide its meaning either: in case I will mention «what I told about yesterday» (thus now) it would make a vicious circle; but even if the form of my future saying ensured that its meaning will exist tomorrow, this would still not provide it today. Regardless my speculations, the actual meaning of expressions yet to be uttered will only arise in their time, from the context that will come.
By lack of interest to describe phrases without their meaning, we'd rather focus on previously uttered expressions, while just "living" the present ones and ignoring future ones. So, my current universe of the past that I can describe today, includes the one I could describe yesterday, but also my yesterday's comments about it and their meaning. I can thus describe today things outside the universe I could describe yesterday. Meanwhile I neither learned to speak Martian nor acquired a new transcendental intelligence, but the same language applies to a broader universe with new objects. As these new objects are of the same kinds as the old ones, my universe of today may look similar to that of yesterday; but from one universe to another, the same expressions can take different meanings.

Like historians, each mathematical theory can only «at any given time» describe a system of past mathematical objects. Its interpretation in this system, «happens» forming a mathematical present outside this realm (beyond this past). Then, describing this act of interpretation, means expanding the scope of our descriptions : the model [T,M] of 1MT, encompassing the interpretations of all expressions of T in the present system M of past objects, is the next realm of the past, coming once the infinite totality of current interpretations (in M) of expressions of T becomes past.

The strength hierarchy of theories

While these successive models are separated by "infinite times", they form an endless succession, reflected by an endless hierarchy between the theories which respectively describe them. This hierarchy will be referred to as a comparison of strength of theories (this forms a preorder). Namely, a theory A is called stronger than a theory B if (a copy of) B can be found as contained in A or a possible development of A; they are as strong if this also goes vice-versa. Indeed, developments are mere "finite moves" neglected by the concept of strength which aims to report "infinite moves" only. (Other definitions of strength order, often but maybe not always equivalent, will come in 2.C).

Many strengths will be represented by versions of set theory, thus letting us call "universes" these successive models. So, any set theory being meant as describing some universe of «all mathematical objects», this merely is at any time the current «everything», made of our past, while this description itself forms something else beyond this «everything».

Strengthening axioms of set theory

While we shall focus on set theories accepting other notions than sets (as announced in 1.4), the difference with traditional set theories (with only sets as objects) can be ignored, as any worthy set theory formalized in our way is as strong as one with only sets, and similarly vice versa.
Our set theories, beyond their common list of basic, "necessary" symbols and axioms (2.1 and 2.2) will mainly differ by strength, according to their choices of optional strengthening axioms (sometimes coming with primitive symbols), whose role will be further commented in 1.D and 2.C. The main strengthening axioms are :

The main foundational theories

As a simplified introduction, here are some of the main foundational theories (all first-order theories, even "second-order arithmetic"), ordered by increasing strength (while infinities of other strengths also exist between and beyond them). The hardest part of Gödel's proof of his famous incompleteness theorems, was to develop TT from Z1, so that the incompleteness results first proven for TT also affect Z1. This difficulty can be skipped by focusing on TT and FST, ignoring Z1. Developing TT from FST is easy (once TT is formalized), but developing either from Z1 is harder. A solution is to develop the "sets only" version of FST from Z1 by defining the BIT predicate (to serve as ∈) and proving its basic properties ; the difficulty to do so can be skipped by accepting these as primitive.

1.B. Truth undefinability

Continuing our introduction to the big picture of the foundations of mathematics, let us sketch a particular aspect of the time ordering of interpretations : the inability of self-describing theories to define (predict) the values of their own statements. This will show the strictness of the strength hierarchy of theories, and will be a key step in the proof of the incompleteness of arithmetic (and thus second-order logic).

Standard objects and quotes

Objects in standard models of a FOT will themselves be called standard, which intuitively means "truly finite" : they can in principle be mathematically quoted, i.e. for each such object x we can form a ground term, here abbreviated by the notation ⌜x⌝, which designates x in the standard model. So, the standard model of arithmetic ℕ is made of standard numbers, values n of quotes ⌜n⌝ looking like 1+...+1 (actual details will be studied in Part 4).
References to the truth of statements and the meaning of classes of FOTs will be implicitly meant as their standard interpretations unless otherwise stated.

Non-standard models can be understood as extensions of the standard one: they still contain all standard objects, i.e. copies of objects of the standard model, defined as values of their mathematical quotes; but differ by having more objects beyond these, called non-standard objects (not quotable). Non-standard numbers will also be called pseudo-finite : they are seen by the theory as «finite» but with the schema of properties of being «absolutely indescribably large» : larger than any standard number, thus actually infinite.
In expressions of statements or classes of foundational theories, it usually makes no difference to allow finite-valued parameters (= whose type belongs to a FOT part of the theory) insofar as they are more precisely meant to only take standard values, and can thus be replaced by their quotes.

In a non-standard model of FST, standard sets are the truly finite sets with only standard elements. But this does not define standardness, which cannot either be defined using quotes (which are infinitely many meta-objects). As will be clear in Part 4, the axiom schema makes standardness undefinable by any formula of FOTs: the meta-set of standard objects in a non-standard model is not a class, and thus (for FST) not a set.

Truth Undefinability theorems

Any well-describable theory T stronger than TT (i.e. able to express TT) can also describe itself : the definitions of the τ, L, X composing T form the development from TT (and thus from T) of the version of 1TT describing T. But this will only be fully used for incompleteness theorems (1.C). First, truth undefinability will need TT (with general notions of expressions) but not X (distinguishing axioms among statements; usual τ and L being finite raise no issues).
(As a bare version of 1TT with undefined τ, L or X would not be a proper development from TT, its working would require to add the use of τ, L, X in the axiom schema : of induction for Z1, or of specification for FST...).

Let S be the meta-class of statements of T, and S the class defined in 1TT and thus in T to play the role of S in any model M of T. For any statement F∈S, its quote ⌜F⌝ designates in M the element of S playing the role of that statement : 1TT⊢ (⌜F⌝∈S).

Let S1 be the meta-class of formulas of T with only one free variable (with range S but this detail may be ignored), meant to define invariant unary predicates over S. Now none of these can match the truth of statements in the same model:

Truth Undefinability Theorem (weak version). For any model M of T, the meta-class {A∈S | M⊨A} of statements true in M, differs from any invariant class, in M, of objects "statements":

∀C∈S1, ∀M⊨T, ∃A∈S, M⊨ (A ⇎ C(⌜A⌝))

Truth Undefinability Theorem (strong version). ∀C∈S1, ∃A∈S, T ⊢ (A ⇎ C(⌜A⌝)).

The tradition focuses on proving the strong version (details in Part 5) : the proof using the liar paradox provides an explicit A, defined as ¬C(⌜A⌝) where the quote ⌜A⌝ is obtained by an explicit (finitistic) but complex self-reference technique. So it gives the "pure" information of a "known unknown" : the necessary failure of C to interpret an explicit A "simply" made of ¬C over a complex ground term.

But the weak version can be proven another way, from the Berry paradox (details involving subtleties in the foundations of arithmetic were moved to Part 4) : from a definition of the truth of statements one can define the predicate between formulas and numbers telling which formula defines which number, and thus define a number in the style of "the smallest number not definable in less than twenty words" which would lead to contradiction.
This proof is both more intuitive (as it skips the difficulties of self-reference), and provides a different information: it shows the pervasiveness of the "unknown unknown" giving a finite range of statements A which are "less pure" in their kind but less complex in size, among which an "error" must exist, without specifying where (it depends on which number would be so "defined").

The hierarchy of formulas

The facts of truth undefinability, undecidability or other indefiniteness of formulas can be understood by analysing their syntax, as mainly coming from their use of binders: the most definite formulas are those without binder ; then, intuitively, the definiteness of a given binder is a matter of how set-like its range is. In set theories, open quantifiers (ranging over the universe or a class) are less definite than bounded quantifiers and other binders whose range is a set.

For FST, the essential condition for a class to be a set is finiteness. Similarly in arithmetic, quantifiers can be bounded using the order : (∃x<k, ) and (∀x<k, ) respectively abbreviate (∃x, x<k ∧ ) and (∀x, x<k ⇒ ) and the same for ≤.
The values of bounded statements of FOTs, are independent of the model as their interpretation only involves standard objects. Any standard object of a FOT has all the same bounded properties (= expressed by bounded formulas with no other free variable) in any model.

Refined versions

The proofs of the truth undefinability theorems, explicitly giving some A on which any C differs from truth, prove more than their mere conclusions: they somehow specify the extent of this difference. Namely : This latter equivalence is done by developing some FOT-bounded quantifiers, thus with finite ranges ; its proof only uses axioms of TT, though C can use a broader language. Therefore if C is definite on the whole class of statements of T, is constant along TT-provably equivalent statements and faithfully processes connectives over instances of C, then C differs from truth on some C(⌜B⌝), i.e.

∃B∈S, C(⌜B⌝) ⇎ C(⌜C(⌜B⌝)⌝)

For either case (weak or strong), in some sense, A needs no more quantifier of any kind than C. So any bounded C differs from truth on some bounded A. In FOTs this is quite a bad difference, but not surprising by lack of bounded candidate truth-approaching C to think of.

Truth predicates

Let us call truth predicate of a theory T described by another theory T', any predicate C (defined by T' with possible parameters) over the class S of statements of T, such that
  1. ∀A∈X, C(A) i.e. it contains all axioms of T
  2. ∀A∈S, C(A)∨C(¬A)
  3. C is consistent.
Equivalently, 2. and 3. can be replaced by
  1. ∀A∈S, C(A) ⇎ C(¬A)
  2. C contains all logical consequences of any conjunction of its own elements.
The existence of a truth predicate of T obviously implies its consistency. But the converse is also provable in TT, making these equivalent:
If T is consistent then a truth predicate of T can be (TT-provably) TT-defined from it in this way:
  1. Take all statements in an arbitrary order;
  2. Add each to axioms if consistent with previously accepted axioms.
Such a definition is not algorithmic (the condition "if consistent" cannot be checked in finite time), but it involves no other parameter than T and an order on its language.

Properties of models

The (first-order) properties of a model M of T, are the statements of T true in M.
The class of properties of any model of T is a truth predicate of T. However this does not always make sense, due to truth undefinability : TT lacks general definitions for the classes of properties of infinite systems. Systematic meaningfulness only comes in strictly stronger frameworks such as MT, able to hold as sets some infinite classes (such as classes of finite objects) serving as types (classes of objects) in M.

Yet the Completeness theorem, while simply expressed in set theories with Infinity, also appears in TT as a schema of theorems, which for any definition of a consistent theory, conceives a model as a class of objects with TT-defined structures. Our simple construction (4.6) ensures the truth of axioms and ignores other statements. By following it, all statements become interpreted as special cases of TT-statements (with parameters τ, L, X composing T, to be replaced by their definitions). The truth predicate so obtained on that class may not be TT-invariant, but is anyway MT-invariant provided that T was (as MT can define truth over the class of TT-statements).

But applying the Completeness theorem to a given truth predicate (which can be TT-defined), proves in TT the existence of a model whose properties conform to it, though its interpreted notions are not sets. This presents in 2 steps how to construct a model with TT-invariant properties, while the same goal is also achieved by the single but harder construction of the traditional proof (by Henkin) of the completeness theorem.

1.C. Introduction to incompleteness

Existential classes

Let us qualify a formula as existential if written ∃x, A(x), with an open ∃ as root (or several, which can be re-expressed as one) followed by a bounded formula A. In this section this will be meant in FOTs only. Existential statements amount to halting conditions of algorithms processed by abstract "computers" with unlimited resources: Similarly, an existential class of a FOT, i.e. defined by an existential formula ∃y, A(y,x), can be equivalently qualified as algorithmically defined, i.e. the range of all outputs given on the way by an endlessly running algorithm; it defines truth over the existential statements obtained from it by replacing x by any quote.

Provability predicates

Provability concepts are linked to existential classes as follows. Usual existential classes of "theorems" among first-order statements with a given language, are formed in 2 steps:
  1. Give a first-order theory with an existential class of axioms (usual ones, including all theories from our list, even have bounded definitions);
  2. Apply there the concept of proof of first-order logic.
The resulting class of theorems is independent of the chosen formal definition for a sound and complete concept of proof in first-order logic, i.e. any two of these leading to FOT-formulas V, V' expressing proof verification for the same theory (defined by symbols τ, L, X), they give the same theorems :

FOT (+ symbols τ, L, X with axioms) ⊢ ∀s, (∃p, V(p,s)) ⇔ (∃p, V'(p,s))

As the first step defines τ, L, X in FOT, it simplifies the above as FOT ⊢ ...

Conversely, if C is an existential class of "theorems" among first-order statements of a theory, and contains the first-order logical consequences of any conjunction of its elements (intuitively, the proving framework contains the power of first-order logic), then C is the class of T-provable statements by first-order logic, for some algorithmically defined first-order theory T : at least trivially, the theory which takes C as its class of axioms.

A theory T stronger than FOT will be qualified as FOT-sound if, on the class of FOT-statements, T-provability implies truth (in the standard model of FOT).

The diversity of non-standard models

Beyond the simple fact of existence of models, the diverse ways to construct them and their use cases (theories) will provide a diversity of models, including non-standard models of foundational theories, more or less similar to standard ones.

Even with identical first-order properties (a condition we can adopt by taking as "axioms" all true statements from a given model, while this is not TT-invariant for standard models of theories containing TT), models can differ by meta-level properties : this will be seen for arithmetic in 4.7, and for any theory with an infinite model by the Löwenheim-Skolem theorem.
But truth undefinability implies that some constructed models also differ from the standard one by first-order properties, because of their invariance. This still goes for "almost complete" foundational theories (e.g. approaching a complete second-order theory by second-order universal elimination).

All foundational theories being FOT-invariant, have models with FOT-invariant properties, thus non-standard already on FOT-properties.
Any consistent MT-invariant T stronger than MT, has MT-invariant (and MT-interpretable) models, thus with a non-standard class of MT-properties (once a concept of "standard model of MT" would be clarified...). Now if T is FOT-sound, adding all true FOT-statements to axioms still forms a consistent and MT-invariant theory, giving models of T with the standard class of FOT-properties despite non-standard other MT-properties (and a most likely non-standard FOT-model).

First incompleteness theorem

Let C be a class of "T-provable" FOT-statements for an algorithmically defined theory T able to express these (i.e. C is an existential class of FOT-statements containing the first-order logical consequences of any conjunction of its elements). By weak truth undefinability, C being FOT-invariant must differ from truth : C(⌜A⌝) ⇎ A for some A.
If T is FOT-sound (C(⌜A⌝) ⇒ A for all A) then for each A on which C differs from truth, A is T-unprovable but true, and thus T-undecidable. Thus T is incomplete (leaving undecidable some FOT-statements). Hence the incompleteness of second-order logic (1.11). This gets close to, yet does not give, the famous

First incompleteness theorem. Any algorithmically defined and consistent theory stronger than FOT is incomplete.

The gap may be overlooked, as it is a worse defect for a theory to be FOT-unsound than to be incomplete. Yet it can be narrowed using our refined version of weak truth undefinability as follows.
Assume T stronger than FOT (i.e. C contains all axioms of FOT, and thus its theorems). Then for all existential A, and thus for A of the form C(B) for any B,

A ⇒ (A is FOT-provable) ⇒ C(⌜A⌝)

If T is consistent and decides all C(A) then C faithfully processes connectives over instances of C (deducing results from proven values of C, may these be incorrect). So: (The literature reports possibilities to prove both incompleteness theorems from the Berry paradox, but these seem very complicated, beyond the scope of this introduction.)

Second incompleteness theorem

The second incompleteness theorem (whose proof uses the strong version of truth undefinability) says C(A) is T-irrefutable for all statements A just if T is consistent :

¬C(⌜0⌝) ⇒ ∀A∈S, ¬C(⌜¬C⌝:A)

where the colon ( : ) means substitution between described expressions so that (⌜B⌝:⌜a⌝) = ⌜B(a)⌝. This is summed up by the case A=⌜0⌝, namely C(⌜¬C(⌜0⌝)⌝) ⇒ C(⌜0⌝) i.e. the consistency of T, if true, is T-unprovable.
Rephrasing this by completeness, if T has no standard contradiction then it has a model which contains a non-standard contradiction (and thus contains no verifiable model).

Also equivalently, T cannot prove the existence of any truth predicate over a notion it describes as the set of its own statements. This is somehow explained, though not directly implied, by weak truth undefinability, which prevents using the current model as an example, since the truth over all standard statements there cannot be T-defined as any invariant predicate (not even speculatively i.e. only working in some models).

Proving times

As the T-provability of any statement A cannot be T-refuted in any way, such as any amount of vain search for T-proofs, that means T keeps "seeing a chance" for A to be T-provable by longer proofs. A theory T' strictly stronger than T can refute the T-provability of some A (such as by finding a T-refutation of A) but remains indecisive on others (such as A = the inconsistency of T').
Any FOT-sound foundational theory (as a knowledge criterion) will always leave some existential statements practically undecidable, may they be actually true or false, the search for proof or refutation appearing vain within given limits of available computing resources : As another aspect of the same fact, provability predicates are inexpressible by bounded formulas (due to truth undefinability, as they are equivalent to truth in the class of bounded statements).
Intuitively, to interpret truth over existential statements (or any T-provability predicate), requires a realistic view : a use of the actual infinity of ℕ specifically meant as its standard interpretation (which cannot be completely axiomatized).

In a kind of paradox, while the completeness theorem is proven by constructing (using actual infinity) a counter example (model) from the fact of absence of proof, there is no "inverse construction" which from the fact about infinities that no system can exist with given properties, would produce any finite witness that is its proof (which must nevertheless exist).
Instead, analyzing this construction can reveal that the size (complexity) of a proof roughly reflects the number of well-chosen elements that must be described in an attempted construction of a counter-example, to discover the necessary failure of such a construction ; the chosen formalization of proof theory can only affect the size of proofs in more moderate (describable) proportions.

1.D. Set theory as a unified framework

Structure definers in diverse theories

Let us call structure definer any binder B which faithfully records the unary structure (relation, resp. function), defined by any input expression (formula, resp. term) A on some range E (type, class or set here fixed), i.e. its result S = (Bx, A(x)) can restore this structure by an evaluator V (symbol or expression) : ∀E x, V(S, x) = A(x).
Admitting the use of negation and the possibility to interpret Booleans by objects (in a range with at least 2 objects, which is often the case), Russell's paradox shows that adding both following requirements on a structure definer in a theory would lead to contradiction :
  1. All such S belong to E
  2. V can occur in the expression A and use x anyhow in its arguments. So V(x, x) is allowed, which is expected as 1. ensures the definiteness of any V(S, S).
Let us list the remaining options. Set theory rejects 1. but keeps 2. But since 1. is rejected, keeping 2. may be or not be an issue depending on further details.

Any generic theory (whose ranges of binders are types) can be legitimately developed (as explained in 4.11) by the construction of a new type K given as the set of all structures defined by a fixed expression A for all combinations of values of its parameters. Indeed a binder with range K abbreviates a successive use of binders on all the parameters of A. Here A and the interpreting model come first, then the range K of structures with its evaluator V are created outside them : A has no sub-term with type K, thus does not use V.

The notion of "structure" in 1MT (one-model theory in first-order logic) has this similarity with the notion of set in set theory : in 1MT, the class of all structures of any fixed symbol type (beyond constants) is usually not a set, calling "sets" such ranges K (of those with a fixed defining expression and variable parameters) and their subsets.
This similarity can be formalized by gathering all such K of the same symbol type (constructed by all possible expressions A) into a single type U, with the same evaluator V (those A might use V but not the range U). This merging of infinitely many ranges into one, merely re-writes what can be done without it, as long as variables of type U are only bound on one of these "sets" K (or equivalently, a range covered by finitely many of them).

In set theory, the ranges of binders are the sets. Thus, beyond its simplifying advantage of removing types, set theory will get more power by its strengthening axioms which amount to accept more classes as sets.

Other theories, which we shall ignore in the rest of this work, follow more daring options:

The unified framework of theories

Like arithmetic (and other FOT), to formalize TT or any 1TT as a complete theory, requires a second-order axiom to exclude non-standard models with pseudo-finite «expressions» and «proofs». Now, the best environment for such second-order theories (giving an appearance of unique determination, though not a real one), and also for MT or 1MT, is the insertion in a strong enough version of set theory (which can define finiteness: see 4.6). As this insertion turns components into free variables which together designate the model, their variability removes the main difference between TT and 1TT, and between MT and 1MT (another difference is that MT can describe inconsistent theories). This development of model theory from a strong enough version of set theory will come in parts 3 and 4, completing the grand tour of the foundations of mathematics after the formalization of set theory (mainly by parts 1 and 2).

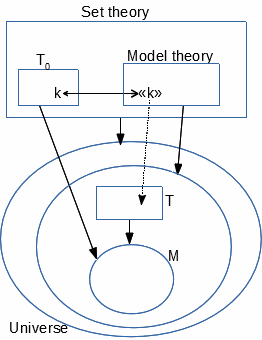Given a theory T so described, let T0 be the external theory, also inserted in set theory, which looks like a copy of T as any component k of T0 is the copy of an object serving as a component of T. In a suitable formalism, T0 can be defined from T as made of the k such that Universe⊨ ⌜k⌝∈T, i.e. the value of the quoting term ⌜k⌝ interpreted in the universe belongs to T.
But there is no general inverse definition, of T from a T0 with infinitely many components, as an object cannot be defined from a given infinity of meta-objects. Any infinite list of components of T0 needs to fit some definition, to get the idealized image T of T0 by interpreting that definition in the universe. (The defining formula must be bounded for T0 to match the above definition from this T).

This forms a convenient framework for describing theories and their models, unifying both previously mentioned set-theoretical and model-theoretical frameworks : all works of the theory T0 (expressions, proofs and other developments), have copies as objects (by interpreting their quotes) formally described by the model theoretical development of set theory as works of the theory T. In the same universe, any system M described as a model of T is indirectly also a (set-theoretical) model of T0.
But as a first-order theory, set theory cannot exclude non-standard universes, whose interpretation of FOTs is non-standard (with pseudo-finite objects). There, the following discrepancies between T0 and T may occur : So understood, the validity conditions of this unified framework are usually accepted as legitimate assumptions, by focusing on well-described theories, interpreted in standard universes whose existence is admitted on philosophical grounds.

Set theory as its own unified framework

Applying this unified framework to the choice of a set theory in the role of T0 (describing M and idealized as an object T), expands the tools of interpretation of set theory into itself (1.7). As T0 co-exists at the same level with the set theory serving as framework, they can be taken as exact copies of each other (with no standardness issue), which amounts to taking the same set theory with two interpretations : M called "universe", and the framework interpretation called "meta-universe".
But the second incompleteness theorem makes them differ as follows. The statement of existence of a universe of any given set theory T (and thus also the stronger statement of existence of a standard one), expressed as a set theoretical statement interpreted in the meta-universe, cannot be a theorem of T. This shows the necessary diversity of strengths between useful axiomatic set theories, which will be further commented in 2.C.

Zeno's Paradox

Achilles runs after a turtle; whenever he crosses the distance to it, the turtle takes a new length ahead.
Seen from a height, a vehicle gone on a horizontal road approaches the horizon.
Particles are sent in accelerators closer and closer to the speed of light.
Can they reach their ends ?
Each example can be seen in two ways: In each example, a physical measure of the «cost» to approach and eventually reach the targeted end, decides which view is «true», according to whether this cost would be finite or infinite (which may differ from the first guess of a naive observer). But the realm of mathematics, free from all physical costs and where objects only play roles, can accept both views.

As each generic theory can use binders over types, it sees types as wholes (sets) and «reaches the end» of its model seen as «closed». But any framework encompassing it (one-model theory or set theory) escapes this whole. Now set theory has multiple models, from a universe to a meta-universe (containing more sets : meta-sets, and new functions between them) and so on (a meta-meta-universe...). To reflect the endless possibilities of escaping any given universe, requires an «open» theory integrating each universe as a part (past) of a later universe, forming an endless sequence of growing realities, with no view of any definite totality. The role of this open theory is played by set theory itself, with the way its expressions only bind variables on sets.

Set theory and foundations of mathematics
Next : 2. Set theory