Aibių teorija ir matematikos pagrindas
1. Pirmieji matematikos pagrindai

1.1 Įvadas į matematikos pagrindus

Kas yra matematika

Matematika yra mokslas apie elementarių objektų sistemas. Šie objektai yra laikomi tiksliais, vienareikšmiais (du objektai yra vienodi ar skirtingi, susiję ar ne; veiksmas duoda tikslų rezultatą). Matematika gali būti laikoma mokslu apie visus galimus tokių tikslių objektų pasaulius.
Matematinės sistemos yra suvokiamos kaip "egzistuojančios" nepriklausomai nuo mums įprasto pasaulio bei pojūčių, bet jų studijavimas reikalauja tam tikro atitikmens. Gali būti naudojami įvairūs būdai, jų rezultatai gali būti tie patys, bet skirtingo tinkamumo (efektyvumo), tai gali priklausyti nuo tikslų. Idėjos gali pirmiausia kilti kaip daugiau ar mažiau vizualios nuojautos, kurios gali būti išreikštos piešiniais ar animacija, o tada jos gali būti išreikštos žodžiais ar formulėmis atidžiam patikrinimui, apdorojimui ir perdavimui. Tam, kad būti laisviems nuo atikmenų ribotumo ir tendencingumo, yra vystomos kitos atitikmenų formos ir susiejamos tarpusavyje jų naudojamos koncepcijos. Matematinis nuotykis yra pilnas virsmų tarp įvairių atitikmenų, kurie gali atspindėti sąsajas tarp pačių matematinių sistemų.

Teorijos

Matematika yra dalinama į šakas pagal sistemų rūšį. Šie bet kurio matematinio darbo rėmai gali arba likti numanomi (su apytikslėmis ribomis) arba formalizuoti kaip teorijos. Kiekviena teorija yra tariamai fiksuotos sistemos, kuri yra tam tikras objektų pasaulis, vadinamas jos modeliu, tyrimas. Bet kiekvienas teorijos modelis gali būti tik viena iš jos galimų interpretacijų, šalia kitų taip pat galimų modelių. Pavyzdžiui, visi popieriaus lapai yra materialių taškų sistemos, tos pačios Euklido plokštumos geometrijos modeliai, bet nepriklausomi vienas nuo kito.

Žodis "teorija" gali būti skirtingos reikšmės, priklausomai nuo to, kur jis naudojamas (matematikoje, kasdieninėje kalboje ar kituose moksluose). Pirmiausia aptarsime jį pagal prigimtį (įprastinius objektus), skirstymas pagal tikslą (realizmas prieš formalizmą) pristatytas žemiau ir 1.9.

Nematematinės teorijos aprašo bendrais bruožais ar smulkiau tam tikras pasaulio sistemas ar aspektus (tyrimo sritis) be tikslaus, išsamaus aprašymo. Pavyzdžiui, įprastuose chemijos aprašymuose daug kas apytiksliai, naudojami iš pažiūros pasirinkti efektai ir dėsniai, kurių dedukcija is kvantinės fizikos dažnai nepasiekiama tiesioginiais skaičiavimais. Aiškaus objektų ir jų sąvybių atskyrimo trūkumas didina klaidų tikimybę, kai dirbama su šiais objektais ir bandoma daryti išvadas iš tam tikrų savybių apie kitas savybes, pavyzdžiui išvadas apie bendras sistemos savybes iš apytikslių jos dalių savybių.

Grynosios matematinės teorijos tik aprašydamos tikslias sistemas paprastai apginamos nuo rizikos būti neteisingomis, naudodamos griežtus metodus (formalias taisykles), skirtus užtikrinti tikslų teorijų atitikimą jų modeliams.

Yra taikomųjų matematinių teorijų, tokių kaip fizikos teorijos, bet matematinės sistemos, kurias jos aprašo, yra kaip idealizuotos (supaprastintos) versijos realaus pasaulio sistemų aspektų; priklausomai nuo tikslumo, ši idealizacija (supaprastinimas iki matematikos) leidžia atlikti teisingą dedukciją priimtinuose klaidos rėmuose.

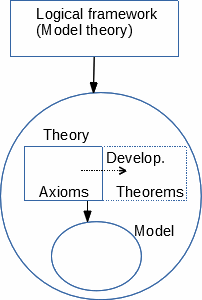Pagrindai ir išvedimas

Bet kuri matematinė teorija, aprašanti savo modelį, yra sudaryta iš turinio ir pati yra aprašoma loginio karkaso. Teorija susideda iš komponentų, kurie yra aprašymo dalys (sąvokos ir informacija aprašyti 1.3). Teorija prasideda nuo pagrindo pasirinkimo. Pagrindas susideda iš loginio karkaso ir turinio pirminės versijos (tikėtina gana nedidelės ar bent jau paprastai aprašomos). Šie pirminės versijos komponentai apibūdinami kaip primityvūs.
Teorijos plėtojimas tęsiamas pasirenkant galimus jos išvedimus : naujus komponentus, kylančius iš esamo jos turinio (vadovaujantis taisyklėmis, aprašytomis loginio karkaso), jie gali būti pridėti prie teorijos ir suformuoti naują turinį. Šie įvairūs turiniai, turintys tą pačią prasmę (aprašantys iš esmės tuos pačius modelius), naudojami skirtingai pateikiant tą pačią teoriją. Kiekvienas kitas galimas teorijos plėtojimas (kuris dar nebuvo pasirinktas) gali būti pridėtas vėliau, nes dalis pagrindų, kurie gali generuoti tokį plėtojimą, lieka. Taip visi galimi teorijos išvedimai, nepriklausomai nuo to, kokia tvarka jie atliekami, jau suformuoja tam tikrą "realybę", kuri yra tiriama.

Tam, kad išreikšti modelių savybes, kiekviena teorija susideda iš eilės teiginių, kurie yra formulės, teisingos prie bet kurio modelio. Paprasčiausi teorijos teiginiai vadinami aksiomomis. Vėlesni teiginiai, kurie vadinami teoremomis, pridedami plėtojant teorijos turinį su sąlyga, kad jie yra išvesti iš ankstesnių: tai užtikrina jų teisingumą su bet kuriais modeliais. Teoremos gali būti panaudotos tolimesniam išvedimui tuo pačiu būdu kaip ir aksiomos. Teorija yra nuosekli, jei jos teoremos niekada neprieštarauja viena kitai. Nenuoseklios teorijos negali turėti jokio modelio, nes teiginys negali būti teisingas ir neteisingas toje pačioje sistemoje. Išbaigtumo teorema (1.9, 1.10, 4.6) parodys, kad visų galimų teoremų visuma tiksliai atitinka tą realybę, kurioje teiginiai išlieka teisingi, esant bet kokiems modeliams (tai būdinga bet kuriai nuosekliai teorijai).
Kiti išvedimo būdai (apibrėžimai ir konstrukcijos), pridedantys kitus komponentus prie teiginių, bus aprašyti 1.5, 1.D, 4.8 ir 4.9.

Galima teorijų hierarchija, kai vienos yra pagrindas kitoms teorijoms. Pavyzdžiui, kelių teorijų pagrindai gali turėti bendrą dalį, suformuojančią paprastesnę teoriją, kurios išvedimai yra pritaikomi visoms teorijoms.
Pagrindinis darbas yra iš paprastos pradinės bazės išvystyti tinkamą žinių visumą kaip labiau visaapimantį pagrindą, turintį efektyvių priemonių, atveriančių labiau tiesioginius būdus tolimesniems dominantiems išvedimams.

Platonizmas prieš formalizmą

Matematika ar bet kuri teorija gali būti aptarta dviem būdais (detaliau 1.9): Daug filosofų ir matematikų turi pasenusių koncepsijų, bet suformuoja ir eilę įvairių priešingų įsitikinimų (pretendentų į tiesą) apie tikrąją matematikos prigimtį. Atlikus tyrimą, lieka tik du būtini ir papildantys požiūriai su skirtingu aktualumu priklausomai nuo temos.

Bet dėl ribotų galimybių žmogaus protas negali visiškai realistiniu būdu dirbti su begalinėmis sistemomis (arba baigtinėmis, bet neriboto dydžio), čia reikia tam tikros logikos ekstrapoliacijai atlikti, apytikriai ekvivalentiškos formaliems samprotavimams, išplėtotiems iš tam tikrų pagrindų; šis formalizavimo darbas gali padėti išvengti galimų intuicijos klaidų. Be to, matematiniai objektai negali suformuoti visiškai baigto, o tik nuolat laikiną, besiplečiantį visetą, kurio tiksli forma susijusi su formalizavimo pasirinkimu.

Nepaisant jo patogumo įrodymų pateikime, grynai formalistinis požiūris negali dominuoti, nes bet kurių pagrindų (starto pozicija su formaliomis plėtojimo taisyklėmis) aiškumas ir savarankiškumas yra reliatyvus: kiekvienas pradžios taškas yra kažkiek pasirenkamas, atsižvelgus ir motyvuojant bendru požiūriu į matematines realijas; jis turi būti apibrėžtas intuityviu, numanomai prasmingu būdu, netiesiogiai pripažįstančiu jo paties pagrindus. Bet kuris bandymas apibrėžti pastarąjį vestų į begalinę regresiją, kurios realus egzistavimas turėtų būti pripažintas.

Pagrindų sritis.

Bendras matematikos pagrindas yra taip pat matematikos tyrimų sritis, taigi ir matematikos šaka, kuri vadinama matematine logika. Nepaisant matematinių objektų paprastos prigimties, tai vis dėlto yra gana sudėtingas mokslas (nors ne tiek, kiek fizikos visko teorija) : aptariant bendrą teorijų ir sistemų, kurios jas gali apibūdinti, formą, suformuojamas bendras visų matematikos šakų karkasas... įskaitant ir bendrus matematikos pagrindus. Taigi būdama visų pagrindų pagrindas (skirtingai nei įprasti matematikos darbai, kuriais einama tolyn nuo numanomo pagrindo), ji nesudaro tikslaus pradžios taško, bet yra plati sritis, sudaryta iš lengvesnių ir sunkesnių žingsnių. Šis sritis iš tikrųjų vaidina pagrindinį vaidmenį matematikoje, aprūpindama įvairias šakas naudingomis koncepcijomis (įrankiais, griežtumu, inspiracijomis ir atsakymais į įvairius filosofinius klausimus).
(Tai panašu į žodyno naudojimą, apibrėžiant kiekvieną žodį per kitus žodžius, ar į kitą mokslą apie sudėtingas tikslias sistemas - kompiuterių programavimą. Kompiuteriai gali būti paprastai naudojami, žinant, kaip tai daryti, bet nenusimanant, kodėl jie veikia; jų veikimas pagrįstas programa, parašyta tam tikra kalba, po to kompiliuota kita programa, be to, įranga ir procesoriumi, kurių dizainui ir gamybai naudotas kompiuteris. Ir šis būdas yra daug geresnis nei programavimo vystymosi pradžioje.)
Dominuoja dvi teorijos:

Kiekvieni yra natūralūs karkasai, formalizuojantys kitus. Kiekviena aibių teorija yra formalizuota kaip teorija, aprašyta modelių teorijos; pastaroji geriau suprantama kaip išplėtojimas iš aibių teorijos (apibrėžiant teorijas ir sistemas kaip kompleksinius objektus) nei tiesiogiai. Abi sąsajos turi būti įvertintos atskirai: abu aibių teorijos vaidmenys - kaip pagrindo ir kaip modelių teorijos tyrimų objekto. Bet toks formalizavimas pareikalaus ilgo darbo.

Next sections only in English and French for now (help needed for translation)
Set theory and Foundations of mathematics
1. First foundations of mathematics
1.1. Introduction to the foundations of mathematics
 ⇨1.2. Variables, sets, functions and operations
1.3. Form of theories: notions, objects, meta-objects
1.4. Structures of mathematical systems
1.5. Expressions and definable structures
1.6. Logical connectives
1.7. Classes in set theory
1.8. Binders in set theory
1.9. Axioms and proofs
1.10. Quantifiers
1.11. Second-order quantifiers
1.A. Time in model theory
1.B. Truth undefinability
1.C. Introduction to incompleteness
1.D. Set theory as unified framework
2. Set theory - 3. Algebra - 4. Arithmetic - 5. Second-order foundations
Other languages:
EN : 1. First foundations of mathematics : 1.1. Introduction to the foundation of mathematics
FR : Introduction au fondement des mathématiques

About this site