1. Premiers fondements des mathématiques

1.1. Introduction aux fondements des mathématiques

Mathématiques

Les mathématiques sont l'étude des systèmes d'objets élémentaires, dont la seule nature considérée est d'être exacts, sans ambiguïté (deux objets sont égaux ou différents, reliés ou non ; une opération donne un résultat exactement...). Les mathématiques dans leur ensemble peuvent être vus comme «science de tous les mondes possibles» de cette espèce (faits d'objets exacts).
Les systèmes mathématiques sont conçus comme «existant» indépendamment de notre monde habituel ou de toute sensation particulière, mais leur étude nécessite une certaine forme de représentation. Diverses méthodes peuvent être utilisées, pouvant être équivalentes (donnant les mêmes résultats) mais avec divers degrés de pertinence (efficacité) pouvant dépendre des objectifs. Les idées apparaissent habituellement comme intuitions plus ou moins visuelles exprimables par des figures ou animations, puis leurs articulations peuvent s'exprimer en mots ou formules pour être attentivement vérifiées, traitées et communiquées. Pour se libérer des limites ou biais d'une forme de représentation particulière, il suffit de développer d'autres formes de représentation, et de s'exercer à traduire les concepts d'une forme à l'autre. L'aventure mathématique est pleine de jeux de conversions entre diverses formes de représentation, qui peuvent refléter les articulations entre les systèmes mathématiques eux-mêmes.

Théories

Les mathématiques se divisent en diverses branches suivant le type de système considéré. Ces cadres de tout travail mathématique peuvent rester implicites (avec des limites floues), ou bien être spécifiés formellement en tant que théories. Chaque théorie est l'étude d'un système (son monde d'objets) supposé fixé, appelé son modèle. Mais chaque modèle d'une théorie peut n'être qu'une de ses interprétations possibles, parmi d'autres modèles également légitimes. Par exemple, en gros, toutes les feuilles de papier sont des systèmes de points matériels, modèles de la même théorie de la géométrie Euclidienne plane, mais indépendants les uns des autres.

Le mot «théorie» peut prendre divers sens suivant les utilisations, de celles mathématiques à celles du langage ordinaire et d'autres sciences. Voici d'abord la distinction suivant leur nature (la sorte générale d'objets); l'autre distinction, par l'intention (réalisme contre formalisme), est introduite plus bas et en 1.9.

Les théories non-mathématiques décrivent grossièrement ou qualitativement des systèmes ou aspects du monde (domaines d'observation), qui échappent à la description simple et exacte. Par exemple, les descriptions habituelles de la chimie utilisent des approximations drastiques, rassemblant de grossières descriptions d'effets et de lois d'apparence arbitraires et dont la déduction de la physique quantique est souvent hors de portée des calculs directs. Le manque de distinction claire des objets et de leurs propriétés induit des risques d'erreurs en les approchant et en essayant de déduire certaines propriétés à partir d'autres propriétés, telles que de déduire certaines propriétés globales d'un système à partir de propriétés floues probables de ses parties.

Les théories de mathématiques pures, décrivant des systèmes exacts, peuvent habituellement être protégées du risque d'être «fausses», par l'usage de méthodes rigoureuses (règles formelles) conçues pour préserver la conformité exacte des théories à leurs modèles voulus.

Entre les deux, les théories de mathématiques appliquées, telles que les théories physiques, sont aussi des théories mathématiques, mais les systèmes mathématiques qu'elles décrivent sont conçus comme versions idéalisées (simplifiées) d'aspects de systèmes donnés du monde extérieur, négligeant d'autres aspects; suivant sa précision, cette idéalisation (réduction à des mathématiques) permet également des déductions correctes dans des marges d'erreur acceptées.

Fondements et développements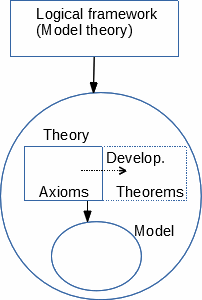

Toute théorie mathématique, décrivant son/ses modèle(s), est faite d’un contenu et est elle-même décrite par un cadre logique. Le contenu d'une théorie est fait de composants qui sont des éléments de description (concepts et informations, décrits en 1.3). Une théorie démarre par le choix d'un fondement formé d'un cadre logique et d'une version initiale du contenu (de préférence petite ou au moins simplement descriptible). Les composants de cette version initiale sont qualifiés de primitifs.
L'étude de la théorie progresse en choisissant certains de ses développements possibles : de nouveaux composants qui résultent de son contenu actuel (par des règles aussi décrites par le cadre logique), et peuvent lui être ajoutés pour former son contenu suivant. Ces différents contenus, ayant la même signification (décrivant essentiellement les mêmes modèles), jouent le rôle de "présentations différentes de la même théorie". Les autres développements possibles (non encore choisis) pourront toujours être effectués plus tard, car la partie du fondement qui pouvait les engendrer subsiste. Dès lors la totalité des développements possibles d'une théorie, indépendante de l'ordre choisi pour les effectuer, forme déjà une sorte de «réalité» que ces développements explorent.

Pour exprimer les propriétés de ses modèles, chaque théorie comprend une liste d'énoncés qui sont des formules annoncées comme vraies dans chaque modèle où elles sont interprétées. Ses énoncés primitifs sont appelés axiomes. D'autres énoncés appelés théorèmes s'ajoutent au contenu par développement, à la condition qu'ils soient prouvés (déduits) à partir des précédents: ceci garantit qu'ils soient vrais dans tous les modèles, du moment que les précédents l'étaient. Les théorèmes sont alors utilisables dans les développements suivants au même titre que les axiomes. Une théorie est cohérente (ou consistante) si ses théorèmes ne se contrediront jamais. Les théories incohérentes ne peuvent avoir aucun modèle, un même énoncé ne pouvaut être vrai et faux sur un même système. Le théorème de complétude (1.9, 1.10, 4.7) montrera que l'ensemble de tous les théorèmes possibles suit précisément la réalité plus intéressante de quels énoncés restent vrais dans tous les modèles (lesquels existent pour toute théorie cohérente).
Les autres sortes de développements (définitions et constructions) ajoutant d'autres composants au-delà des énoncés, seront décrits en 1.5, 1.D, 4.10 et 4.11.

Il y a des hiérarchies possibles entre théories, certaines pouvant jouer un rôle fondateur pour d'autres. Notamment, les fondements de plusieurs théories peuvent avoir une partie commune formant une théorie plus simple, dont les développements sont applicables à toutes.
Un travail fondamental est de développer, à partir d'une base initiale simple, un corps de connaissances commodes pour servir de "fondement" plus complet, muni d'outils efficaces ouvrant des voies plus directes vers d'autres développements intéressants.

Platonisme vs Formalisme

Les mathématiques, ou chaque théorie, peuvent être abordées de deux manières (détaillées en 1.9). De nombreux philosophes des mathématiques ont des conceptions obsolètes de telles idées comme formant une liste de multiples croyances opposées (vérités candidates) sur la nature réelle des mathématiques. Mais après examen, il ne reste que ces deux approches nécessaires et complémentaires, avec diverses parts de pertinence suivant les sujets:

Par ses capacités limitées, la pensée humaine ne peut pas opérer d'une manière pleinement réaliste sur les systèmes infinis (ou des systèmes finis de taille illimitée), mais nécessite une sorte de logique d'extrapolation, grossièrement équivalente à des raisonnements formels développés à partir de certains fondements; ce travail de formalisation permet d'éviter d'éventuelles erreurs de l'intuition. De plus, les objets mathématiques ne peuvent pas former une totalité achevée, mais seulement un domaine toujours temporaire, en expansion, dont la forme précise est une apparence relative à un choix de formalisation.

Mais au-delà de son incommodité à exprimer les preuves, une vision purement formaliste ne serait pas non plus tenable car la clarté et l’autosuffisance de tout fondement possible (position de départ avec des règles de développement formelles) restent relatives: tout point de départ a dû être choisi plus ou moins arbitrairement, issu de et motivé par une perspective plus large sur les réalités mathématiques; il doit être défini d'une manière intuitive, supposément claire, admettant implicitement son propre fondement, car toute tentative de préciser ce dernier conduirait à une régression sans fin, dont la préexistence réaliste devrait être admise.

Le cycle des fondements

Le fondement général de toutes les mathématiques est lui-même une étude mathématique, donc une branche des mathématiques appelée la logique mathématique. Malgré la simplicité de nature des objets mathématiques, il s'avère assez complexe (quoique moins qu'une théorie du tout de la physique): en décrivant la forme générale des théories et des systèmes qu'elles peuvent décrire, il forme le cadre général de toutes les branches des mathématiques... lui-même inclus. Ainsi fournissant le fondement de chaque fondement considéré (à l'inverse des travaux mathématiques ordinaires avançant à partir d'un fondement admis), il ne forme pas un point de départ précis, mais une vaste boucle composée d'étapes plus ou moins difficiles. Néanmoins, ce cycle joue bien un rôle fondateur pour les mathématiques, fournissant à ses diverses branches de nombreux concepts utiles (outils, rigueur, inspirations et réponses à diverses questions philosophiques).
(Cette situation ressemble au rôle des dictionnaires définissant chaque mot par d'autres mots, ou à cette autre science des systèmes complexes exacts: l'informatique. On peut en effet simplement utiliser les ordinateurs, sachant ce qu'on fait mais non pourquoi cela fonctionne; leur fonctionnement se base sur des logiciels qui furent rédigés dans un certain langage puis compilés par d'autres logiciels, et sur le matériel et le processeur dont la conception et la fabrication furent assistées par ordinateur. Et c'est nettement mieux ainsi qu'à la naissance de cette discipline.)
Il est dominé par deux théories:

Chacune est le cadre naturel pour formaliser l'autre: toute théorie des ensembles se formalise comme théorie décrite par la théorie des modèles; celle-ci vient mieux comme développement de la théorie des ensembles (définissant théories et systèmes comme objets complexes), que directement comme théorie. Ces deux liens doivent être considérés séparément : les deux rôles de la théorie des ensembles, comme cadre et comme objet d'étude pour la théorie des modèles, doivent être distingués. Mais ces formalisations nécessiteront un long travail pour être complétées.

1.2. Variables, ensembles, fonctions et opérations

Un démarrage des mathématiques consiste à introduire quelques concepts simples du cycle fondateur, pouvant sembler auto-suffisants autant que possible alors qu'ils ne peuvent pas l'être absolument (faute de définitions claires qui nécessiteraient un démarrage différent). Une solution habituelle et naturelle est de démarrer par une théorie des ensembles non totalement formalisée comme théorie axiomatique.

Cette section (1.2) introduira intuitivement quelques premiers concepts de la théorie des ensembles : ceux d'ensemble, de fonction et d'opération. Mais il commencera par introduire quelques qualifications de variables conçues comme des qualités extrinsèques, à savoir visant à décrire le statut d'une variable donnée par rapport à certains types de contextes (points de vue) qui ne sont pas encore eux-mêmes introduits à ce stade. Le lecteur est invité à ne pas se laisser arrêter par cette forme d'imprécision qui se résoudra probablement au fil des utilisations spécifiques dans les sections suivantes.

Puis 1.3 commencera à introduire la théorie des modèles, par laquelle toute théorie (et donc toute théorie des ensembles) est formalisable. D'autres subtilités (paradoxes) dans la vision globale des fondements des mathématiques seront expliquées ultérieurement.

Constantes

Un symbole de constante est un symbole désignant un objet précis, appelé sa valeur. Exemples: 3, Ø, ℕ. Ceux du langage courant se présentent habituellement comme noms propres et noms avec un article défini singulier («le», «la») sans complément.

Variables libres et liées

Un symbole de variable (ou une variable) est un symbole qui, au lieu d'avoir une valeur donnée a priori, vient avec le concept de valeurs possibles, ou d'interprétations possibles dont chacune lui donne une valeur particulière. Chaque possibilité lui donne un rôle de constante. Ces possibilités peuvent être en nombre quelconque, y compris une infinité, une seule ou même aucune.
On peut l'imaginer comme délimité par une boite dont l'intérieur a plusieurs versions en parallèle, articulant les différents points de vue à son sujet: Plus précisément par rapport à des théories données, fixer une variable signifie prendre une variable libre dans une théorie et ignorer plus longuement sa variabilité, simulant ainsi l'utilisation de l'autre théorie obtenue en acceptant ce symbole comme une constante.
Les divers «points de vue internes», correspondant à chaque valeur possible vue comme fixe, peuvent être considérés comme des «lieux» abstraits dans l'univers mathématique, tandis que la succession de points de vue sur un symbole (le qualifiant comme constante, variable libre ou variable liée), peut être vue comme une première expression de l'écoulement du temps en mathématiques: une variable est liée lorsque tous les «lieux parallèles de l'intérieur de la boite» (valeurs possibles) sont passés. Tous ces lieux et temps sont eux-mêmes des entités purement abstraites et mathématiques.

Domaines et ensembles

On appelle domaine d'une variable, sa signification vue comme liée: c'est la «connaissance» de la totalité considérée de ses valeurs possibles ou autorisées (vues en vrac: sans ordre ni égard à leur contexte) appelées les élements de ce domaine. Cette «connaissance» est une entité abstraite éventuellement capable (suivant le contexte) de traiter (englober) des infinités d'objets (contrairement à l'esprit humain). Tout domaine d'une variable est appelé un ensemble.
Une variable admet un domaine lorsqu'elle peut être liée: lorsqu'un point de vue englobant toutes ses valeurs possibles est donné. Les variables de la théorie des ensembles n'auront pas toutes un domaine. Une variable sans domaine peut toujours être libre, ce qui n’est plus un statut intermédiaire entre fixe et liée, mais signifie qu’elle peut prendre certaines valeurs ou d’autres valeurs sans prétention d’exhaustivité.

Cantor définissait un ensemble comme «un groupement en un tout d'objets bien distincts de notre intuition ou de notre pensée». «Si la totalité des éléments d'une multiplicité peut être pensée comme «existant simultanément», de telle sorte qu'il soit possible de la concevoir comme un «seul objet» (ou un «objet achevé»), je la nomme une multiplicité consistante ou un «ensemble».» (Nous venons d'exprimer cette «multiplicité» comme celle des valeurs d'une variable).
Il décrivit le cas contraire comme celui d'une «multiplicité inconsistante» où «l'admission d'une coexistence de tous ses éléments mène à une contradiction». Mais la non-contradiction ne peut pas suffire comme définition générale des ensembles: la non-contradiction d'un énoncé n'implique pas sa véracité (l'énoncé contraire peut être vrai mais indémontrable); les faits de non-contradiction sont souvent eux-mêmes indémontrables (théorème d'incomplétude), et deux coexistences séparément consistantes pourraient se contredire (paradoxe de l'omnipotence).

On dit qu'une variable parcourt un ensemble, lorsqu'elle est liée de domaine cet ensemble. On peut introduire à volonté des variables parcourant tout ensemble donné, indépendantes entre elles et des autres variables en présence.
Le renommage systématique d'une variable liée dans tout l'intérieur de sa boite, en un autre symbole inutilisé dans le même contexte (la même boite), de même domaine, ne change pas la signification du tout. En pratique, une même lettre peut représenter plusieurs variables liées séparées (dont les boites sont séparées), qui peuvent prendre des valeurs différentes sans incohérence : il ne s'en trouve nulle part deux libres à la fois où l'on puisse en comparer les valeurs. Le langage courant le fait sans cesse, ne disposant que de fort peu de symboles de variables («il», «elle», ...).

Fonctions

Une fonction est un objet f constitué des données suivantes: Ainsi f est une entité se comportant comme variable dont la valeur est déterminée par celle d'une autre variable appelée son argument de domaine Dom f. Dès que cet argument est fixé (reçoit un nom, ici "x", et une valeur dans Dom f), f devient fixe, notée f(x). Cela revient en fait à concevoir une variable f dont les "vues possibles" comme fixe, sont traitées comme des objets x conceptuellement distincts de la valeur résultante de f. Comme nous le verrons plus tard, une telle entité (variable dépendante) f ne serait pas (traitable comme) un objet de la théorie des ensembles si son argument n'avait pas de domaine, autrement dit ne pouvait pas être lié. (Ce ne serait qu'un méta-objet, ou objet de la théorie des modèles, qu'on appellera un foncteur en 1.4)

Opérations

La notion d'opération généralise celle de fonction, par l'admission d'une liste finie d'arguments (variables de domaines respectifs donnés) au lieu d'un seul. Une opération donne donc un résultat (une valeur) quand tous ses arguments sont fixés. Le nombre n des arguments d'une opération est appelé son arité ; l'opération est dite n-aire. Elle est dite unaire si n=1 (c'est une fonction), binaire si n=2, ternaire si n=3...
Le concept d'opération nullaire (n=0) est superflu, car leur rôle est déjà joué par leur unique valeur; on verra en 2.1 comment construire les opérations d'arité > 1 au moyen des fonctions.

Comme pour les fonctions, les arguments des opérations sont à la base désignés non par des symboles mais par des espaces autour du symbole d'opération, à remplir par toute expression leur donnant les valeurs voulues. Diverses conventions d'écriture peuvent être utilisées (1.5). Notamment, en utilisant les espaces à gauche et à droite dans la parenthèse après le symbole f, on note f(x,y) la valeur d'une opération binaire f en ses arguments fixés x et y (sa valeur lorsque ses arguments reçoivent les valeurs fixes de x et y).

Un urelement (élément pur) est un objet ne jouant aucun autre rôle que celui d'élément: ce n'est ni un ensemble, ni une fonction, ni une opération.

1.3. Forme des théories: notions, objets et méta-objets

La variabilité du modèle

Chaque théorie décrit son modèle comme un système fixe. Mais du point de vue plus large de la théorie des modèles, cela n'est qu'un simple «choix» d'un modèle (interprétation) possible dans une diversité (généralement infinie) d'autres modèles existants, également légitimes, de la même théorie. Or, cette fixation du modèle, comme la fixation de toute variable, n’est que le simple acte de choisir une possibilité, en ignorant toute question de savoir comment spécifier un exemple. En fait, ces «choix» et «existence» de modèles peuvent être très abstraits. En détail, la preuve du théorème de complétude «spécifiera» effectivement un modèle de toute théorie cohérente pour le cas général, mais cette définition ne sera pas très explicite, par son usage de l'infini. Sans égard à cette difficulté, l’attitude de fixer implicitement un modèle lorsqu’on étudie formellement une théorie mathématique, reste la manière normale de l'interpréter (sauf en un sens pour la théorie des ensembles comme expliqué en 2.A).

Notions et objets

Chaque théorie a sa propre liste de notions (couramment désignées par des noms communs), qui lui servent formellement de sortes de variables utilisables. Chaque modèle interprète chaque notion comme un ensemble qui est le domaine commun de toutes les variables de cette sorte. Par exemple, la géométrie euclidienne a les notions de «point», «ligne droite», «cercle» et plus, et est habituellement exprimée en utilisant un style différent de symboles de variables pour chacune. Les objets d'une théorie dans un modèle, sont toutes les valeurs possibles de ses variables de toutes sortes (éléments de toutes ses notions) dans ce modèle.

Théorie du modèle

Toute discussion sur plusieurs théories T et systèmes M modèles possibles de ces T, s'effectue dans la théorie des modèles, avec ses notions de «théorie» et «système» qui sont les sortes respectives des variables T et M. Mais en se concentrant sur une théorie avec un modèle fixe, les variables T et M étant fixées disparaissent de la liste des variables. Leurs sortes, les notions de théorie et de modèle, disparaissent ainsi de la liste des notions. Ceci réduit le cadre, d'une théorie des modèles à une théorie du modèle.
Un modèle d'une théorie du modèle, est un système [T,M] combinant une théorie T et un modèle M de T.

Sur la diversité des cadres logiques

Le rôle d'un cadre logique, version précise de la théorie du modèle ou des modèles avec sa théorie des preuves, est de décrire Voici ceux que nous présenterons, grossièrement ordonnés du plus pauvre au plus expressif (bien que l'ordre dépende des manières de les relier): Nous allons d'abord décrire les deux principaux cadres logiques en parallèle. La logique du premier ordre est la version la plus courante de la théorie des modèles, décrivant les théories du premier ordre que nous appellerons également théories génériques. La théorie des ensembles, qui peut englober toutes les autres théories, pourra également englober les cadres logiques et ainsi servir elle-même de cadre logique ultime, comme sera expliqué en 1.D.
Le qualificatif "ensembliste" visera à qualifier tout concept appartenant à, ou se rapportant à, la théorie des ensembles.
La plupart des cadres gèrent les notions comme des types (habituellement en nombre fini pour chaque théorie), classifiant à la fois variables et objets. Les notions sont appelées des types si chaque objet n'appartient qu'à un seul d'entre eux, qu'on appelle alors aussi le type des variables qui peuvent le désigner. Par exemple, un objet de la géométrie euclidienne peut être un point ou une droite, mais le même objet ne peut être à la fois un point et une droite. Mais la théorie des ensembles aura besoin d'autres notions que les types: les classes, qui seront introduites en 1.7.

Exemples de notions de diverses théories

Théorie Sortes d'objets (notions)
Théorie générique Urelements classés par types pour jouer divers roles
Théorie des ensembles  Eléments, ensembles, fonctions, opérations, relations, uplets...
Théorie des modèles Théories, systèmes et leurs composants (détaillés ci-dessous).
Théorie du modèle Objets, symboles, types ou autres notions, Booléens,
structures (opérateurs, prédicats), expressions (termes, formules)...
Arithmétique Nombres entiers
Algèbre linéaire Vecteurs, scalaires...
Géométrie Points, droites, cercles...

Méta-objets

Les notions d'une théorie du modèle (1MT), normalement interprétées dans [T,M], classifient les composants de T («type», «symbole», «formule»...) et ceux de M («objet», et des outils pour y interpréter les composants et expressions de T). Mais les mêmes notions (pouvant appartenir à un autre cadre logique) pourront être interprétées dans [1MT, [T,M]], en les marquant du préfixe méta-.

Par sa notion d'«objet», chaque théorie du modèle distingue les objets de T dans M, du reste de ses propres objets dans [T,M] qui sont les méta-objets. La règle ci-dessus d'utilisation du préfixe méta admettrait tout objet comme un méta-objet ; mais on fera une exception de vocabulaire en réservant le nom de méta-objet à ceux qui ne sont pas des objets : symboles, types ou autres notions, Booléens, structures, expressions...

La théorie des ensembles ne connait que les domaines de certaines de ses variables, vus comme objets (ensembles). Mais, vue par la théorie du modèle, toute variable d'une théorie a un domaine parmi les notions, qui ne sont que des méta-objets.

Composants des théories

Dans un cadre logique donné, le contenu d'une théorie consiste en 3 listes de composants de sortes suivantes, où ceux de chacune des 2 dernières sortes sont des systèmes finis utilisant ceux de la sorte précédente:

Interprétation ensembliste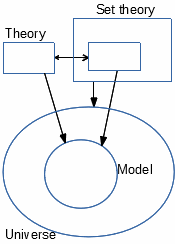

Toute théorie générique peut être interprétée (insérée, traduite) en théorie des ensembles, en convertissant ses composants en composants de la théorie des ensembles. C'est l'approche habituelle des mathématiques ordinaires, voyant de nombreux systèmes comme «ensembles avec des relations ou des opérations telles que ...», avec des connexions possibles entre ces systèmes. Introduisons à la fois les interprétations génériques applicables à toute théorie générique, et d'autres habituellement préférées pour certaines théories spécifiques.

Toute interprétation convertit chaque type abstrait en un symbole (nom) désignant un ensemble appelé type interprété (servant de domaine aux variables de ce type, dont l'usage reste par ailleurs intact). Ce symbole est habituellement une variable fixe dans le cas générique, mais peut être accepté comme symbole de constante de la théorie des ensembles dans des cas spéciaux comme les systèmes de nombres (ℕ, ℝ...).
Dans les interprétations génériques, tous les objets (éléments des types interprétés) sont des urelements, mais d'autres sortes d'interprétations dites standard par convention pour des théories spécifiques peuvent faire autrement. Par exemple, les interprétations standard de la géométrie représentent les points par des urelements, mais représentent les droites par des ensembles de points.

Les interprétations génériques convertiront aussi les symboles de structure en variables fixes (tandis que celles standard peuvent les définir par le langage de la théorie des ensembles). Tout choix de valeurs fixes de tous les types et symboles de structure, définit un choix de système. Lorsque le langage est vu comme un ensemble (en particulier s'il est fini) ce qui est généralement le cas, les modèles sont eux-mêmes des objets de la théorie des ensembles, dont la multiplicité vient de la variabilité des types et des symboles de structures. Ceci permet d'intégrer toutes les théories voulues dans une même théorie des ensembles, en rassemblant des représentants de tous leurs modèles considérés dans un même modèle de la théorie des ensembles. C'est pourquoi les modèles de la théorie des ensembles sont appelés des univers.

En adoptant la théorie des ensembles comme notre cadre conceptuel, ce concept "d'interprétation" devient synonyme de choix (désignation) d'un modèle.

1.4. Structures des systèmes mathématiques

Les structures, désignées dans chaque interprétation par les symboles de structure formant un langage donné, forment un système décrit en reliant les objets des différents types, donnant leurs rôles aux objets de chaque type en rapport avec ceux d'autres types. Suivant les détails, les rôles ainsi donnés aux objets de certains types peuvent être compris comme ceux d'objets complexes, bien que tout cela puisse fonctionner avec de simples objets comme des urelements.

Structures du premier ordre

Les sortes de structures (et donc aussi les sortes de symboles de structure) autorisées dans les théories du premier ordre, ainsi appelées structures du premier ordre, se divisent en opérateurs et prédicats comme décrit plus bas. Des structures plus puissantes nommées structures du second ordre seront introduites en 5.1, venant d'outils ensemblistes ou comme paquets d'un type supplémentaire avec des structures du premier ordre.
Un opérateur est une opération entre des types interprétés. Au niveau de la théorie avant interprétation, chaque symbole d'opérateur vient avec son type de symbole formé de Dans une théorie avec un seul type, cette donnée est réduite à l'arité.
Les symboles de constantes d'une théorie sont ses symboles d'opérateur nullaires (sans argument).
Les opérateurs unaires (qui sont des fonctions) seront appelés ici des foncteurs (*).

La liste des types est complété par le type booléen, interprété comme la paire d'éléments (l'ensemble de deux éléments) qu'on notera 1 pour «vrai» et 0 pour «faux». Une variable de ce type (hors de la théorie) est appelée une variable booléenne.

Un para-opérateur est un opérateur au sens généralisé autorisant le type Booléen parmi ses types d'arguments et de résultats.
Un connecteur est un para-opérateur dont tous les arguments et les valeurs sont booléens.
Un prédicat est un para-opérateur à valeurs booléennes avec au moins un argument mais aucun argument booléen.

Structures de la théorie des ensembles

Formaliser la théorie des ensembles, c'est la décrire comme une théorie avec ses notions, ses structures et ses axiomes. Nous le ferons dans un cadre logique dédié, distinct mais convertible en logique du premier ordre par une procédure décrite en 2.1.
Ceci relie les terminologies de la théorie des ensembles et de la théorie du modèle, de manière différente de lorsqu'une théorie est interprétée en théorie des ensembles. Pour garder les noms naturels des notions ensemblistes (ensembles, fonctions ...) lorsqu'on les définit par cette formalisation, il deviendrait incorrect de les utiliser encore au sens du lien précédent (où les notions étaient des "ensembles" et les opérateurs étaient des "opérations"). Pour éviter toute confusion, utilisons ici uniquement les notions de théorie des modèles comme notre cadre conceptuel, ignorant leurs interprétations ensemblistes. Les manières de rassembler ces deux liens, et de réconcilier les deux conceptions des mêmes théories (descriptions par la théorie des modèles et interprétations ensemblistes), seront décrites en 1.7 et 1.D.

Admettons 3 notions primitives : éléments (tous les objets), ensembles et fonctions. Voici leurs principales structures primitives.
Un aspect du rôle des ensembles, est donné par le prédicat binaire ∈ d'appartenance : pour tout élément x et tout ensemble E, on dit que x est dans E (ou x appartient à E, ou x est élément de E, ou E contient x), et on note x ∈ E, pour signifier que x est une valeur possible des variables de domaine E.
Les fonctions f jouent leur rôle par deux opérateurs : le foncteur Dom (donnant leurs domaines) et l'évaluateur de fonctions, opérateur binaire implicite dans la notation f(x), d'arguments f et x, et donnant la valeur de toute fonction f en tout élément x de Dom f.

D'autres symboles primitifs seront présentés en 1.7 et 1.8, puis la plupart des autres symboles primitifs et axiomes seront introduit en 1.A, 2.1, 2.2 et 2.7.

A propos de la théorie axiomatique des ensembles ZFC

La théorie des ensembles de Zermelo-Fraenkel (ZF, ou ZFC avec axiome du choix) est une théorie générique avec un seul type «ensemble», le symbole de structure ∈, et des axiomes. Il suppose implicitement que tout objet est un ensemble, et donc un ensemble d'ensembles indéfiniment, construits sur l'ensemble vide.
Comme théorie des ensembles assez simplement exprimable mais très puissante pour un cycle fondateur élargi, elle peut en effet être un bon choix pour les spécialistes de logique mathématique pour prouver commodément divers théorèmes fondationnels difficiles, tels que la non-démontrabilité de certains énoncés, tout en leur donnant une portée sans doute parmi les meilleures concevables.
Mais malgré l’habitude des auteurs de cours de mathématiques de base de concevoir leur présentation de la théorie des ensembles comme une version vulgarisée ou implicite de ZF(C), ce n’est en fait pas une référence idéale pour un démarrage des mathématiques pour débutants:

Formalisation des types et structures comme objets de la théorie du modèle

Pour formaliser la théorie du modèle en utilisant le préfixe méta-, les méta-notions de "types" et de "structures" reçoivent leurs rôles par des méta-structures comme suit.

La théorie du modèle supposant une modèle fixe, il lui suffit d’un méta-type de "types" pour jouer les deux rôles de types abstraits (dans la théorie) et de types interprétés (composants du modèle), respectivement donnés par deux méta-foncteurs: l'un des variables vers les types, et l'autre des objets vers les types. En effet, la notion plus générale d'«ensemble d'objets» n'est pas utilisée et peut être ignorée.

Mais la méta-notion de structure devra rester distincte du langage, car d'autres structures que celles nommées dans le langage seront employées (1.5). Les structures recevront leurs rôles d'opérations, par des méta-structures similaires à l'évaluateur de fonctions (voir 3.1-3.2 pour une approche), tandis que le langage (ensembles des symboles de structure) y sera interprété par un méta-foncteur des symboles de structure vers les structures.
Or, cette seule formalisation laisserait indéterminée l'étendue de cette notion de structure. Essayer de concevoir cette étendue comme celle de «toutes les opérations entre les types interprétés» laisserait inconnue la source de connaissance d'une telle totalité. Cette idée de totalité sera formalisée en théorie des ensembles par l'ensemble des parties (2.5), mais sa signification dépendra encore de l'univers où il est interprété, loin de notre préoccupation actuelle pour la théorie du modèle.

1.5. Expressions et structures définissables

Termes et formules

Etant donnés les deux premiers niveaux d'une théorie (une liste de types et un langage), une expression est un système fini d'occurrences de symboles, où, intuitivement parlant, une occurrence d'un symbole dans une expression est un lieu où ce symbole est écrit (détails plus loin).

Chaque expression vient dans le contexte d'une liste de variables libres disponibles donnée. Toute expression définira une valeur (un objet ou un Booléen) pour chaque donnée possible de:

Le type d'une expression, déterminé par sa syntaxe comme décrit plus bas, sera le type de ses valeurs. Les expressions de type booléen sont des formules ; les autres, de type appartenant à la liste des types donnés (leurs valeurs seront des objets), sont appelés des termes.

Par exemple « x+x » est un terme comportant 2 occurrences de la variable «x», et une du symbole d'addition «+».

Les diverses sortes de symboles

Les expressions des théories du premier ordre et de la théorie des ensembles, peuvent utiliser les symboles des sortes suivantes. En logique du premier ordre, appelons symboles logiques les quantificateurs et symboles de para-opérateur hors du langage (égalité, connecteurs et opérateur conditionnel): leur liste et leur signification dans chaque système sont déterminés par le cadre logique et la liste de types donnée, ce qui justifie de ne pas les présenter comme composants de théories particulières.

Racine et sous-expressions

Chaque expression contient une occurrence spéciale d'un symbole appelé sa racine, chaque autre occurrence d'un symbole dedans étant la racine d’une unique sous-expression (une autre expression qu’on peut appeler la sous-expression de cette occurrence). Le type d'une expression est donné par le type de résultats de sa racine.

Les expressions se construisent successivement, en parallèle entre différentes listes de variables libres disponibles. Les premières et plus simples sont faites d'un seul symbole (comme racine, ayant déjà une valeur par lui-même) : les symboles de constante et de variable sont les premiers termes; les constantes booléennes 1 et 0 sont les plus simples formules.
Les autres expressions se construisent successivement comme formées des données suivantes :

Un terme algébrique est un terme n'utilisant que des variables libres et des symboles d'opérateur ; ce sont les seuls termes en logique du premier ordre sans opérateur conditionnel. Cette notion pour un seul type, sera formalisée comme une sorte de système en théorie des ensembles en 4.1.

Conventions d'écriture

La présentation de cette liste de sous-expressions directement attachées à la racine nécessite un choix de convention. Pour un symbole de para-opérateur autre qu'une constante : Les parenthèses peuvent aussi servir à distinguer (séparer) les sous-expressions, donc distinguer la racine de chaque expression parmi les autres occurrences de symboles. Par exemple la racine de (x+y)n est l'opérateur de puissance.

Structures variables

Seuls quelques objets sont habituellement nommés par les symboles de constantes d'un langage donné. Tout autre objet peut être nommé par un symbole de variable fixe, dont le statut dépend du choix de la théorie dans laquelle on se place: La différence disparait dans les interprétations génériques qui convertissent les constantes en variables (dont les valeurs définissent différents modèles).
Par analogie avec les constantes qui sont des structures particulières (opérateurs nulaires), le concept de variable se généralise en celui de structure variable. Mais ceux au-delà des opérations nulaires échappent à la liste ci-dessus des symboles admis dans les expressions. Cependant, certains types d'utilisation de symboles de structure variable peuvent être justifiés comme d'abréviations (descriptions indirectes) de l'utilisation d'expressions légitimes. Le cas principal de ceci est expliqué ci-dessous; un autre usage (qui y ressemble mais est en fait celui d'une méta-variable) viendra en 1.10.

Structures définies par des expressions

Partant de n'importe quelle théorie on peut introduire une sorte de symbole de structure variable (opérateur ou prédicat, même si un prédicat nulaire est habituellement appelé une "variable booléenne" au lieu d'une "structure"), définie par les données suivantes qu'il vise à abréger : Chacune de ses valeurs possibles comme structure ou Booléen vient en fixant les valeurs des paramètres. Ainsi, la variabilité d'un tel symbole est l'abréviation de celle de tous les paramètres.
Toute théorie peut se développer par la construction d'une nouvelle notion (type abstrait) donné comme domaine d'une structure variable définie par une expression donnée, lorsque ses paramètres parcourent toutes leurs combinaisons de valeurs possibles. Tel est notre premier cas d'une règle de construction (sorte de développement d'une théorie). La revue complète des règles de construction sera présentée en 4.11.

En théorie des ensembles, toute fonction f est synonyme du foncteur défini par le terme «f(x)» d'argument x et de paramètre f (mais le domaine de ce foncteur est Dom f au lieu d'un type). Les termes sans argument définissent de simples objets (opérateurs nulaires); celui fait d'une variable d'un type donné, vu comme paramètre, suffit pour donner tous les objets de ce type.

Déclarons maintenant la méta-notion de "structure" en théorie du modèle, et donc celles d '"opérateur" et de "prédicat", comme devant contenir toutes les structures ainsi atteignables: définies par toute expression avec toutes les valeurs possibles des paramètres. La version minimale d'une telle méta-notion peut être formalisée comme un rôle donné à l'ensemble de toutes les combinaisons d'une expression avec des valeurs fixes de ses paramètres. Comme cela fait appel à l'ensemble infini de toutes les expressions, cette méta-notion échappe habituellement (est inaccessible) aux capacités de la théorie étudiée : aucune expression fixe ne peut suffire à la simuler. De plus en interprétant cela en théorie des ensembles, encore d'autres d'opérations (indéfinissables) entre types interprétés existent généralement dans l'univers. Parmi les rares exceptions, le domaine ensembliste complet d'une structure variable dont tous les arguments parcourent des ensembles finis (comme types interprétés) avec des limites de taille données, peut être atteinte par une expression dont la taille dépend de ces limites.

Structures invariantes

Une structure invariante d'un système donné (langage interprété), est une structure définie à partir de son langage sans paramètre (donc constante). Cette distinction des structures invariantes parmi les autres structures, généralise la distinction entre les constantes et les variables, à la fois aux cas d'arité non nulle, et à ce qui peut être défini par des expressions plutôt que directement nommé dans le langage.

En effet toute structure désignée par un symbole du langage est directement définie par lui sans paramètre, et donc invariante. Comme sera détaillé en 4.10, les théories peuvent être développées par des définitions, consistant à nommer une autre structure invariante par un nouveau symbole ajouté au langage. Parmi les aspects de la signification préservée de la théorie, figurent les méta-notions de structure, structure invariante, et l'ensemble des théorèmes exprimables avec le langage précédent.

1.6. Connecteurs logiques

Nous avons défini précédemment le concept de connecteur logique. Énumérons maintenant les principaux connecteurs utiles, au-delà des deux connecteurs nullaires (constantes booléennes) 1 et 0. (A cela s'ajoutera le connecteur conditionnel en 2.1).

Tautologies

Leurs propriétés seront exprimées par des tautologies, qui sont des formules utilisant uniquement des connecteurs et des variables Booléennes (ici écrites A, B, C), et vraies pour toutes les combinaisons de valeurs possibles de ces variables. Ainsi, les tautologies donnent également des formules nécessairement vraies après remplacement de ces variables par des formules les définissant utilisant n'importe quel langage et interprétées dans tout système. De telles définitions des variables booléennes par les formules d'une théorie peuvent restreindre leurs domaines de valeurs possibles dépendant les unes des aux autres.

Les tautologies constituent les règles de l'algèbre booléenne, une théorie algébrique décrivant les opérations sur le type booléen, lui-même naturellement interprété comme la paire d'éléments 0 et 1 (mais admettant également des interprétations plus sophistiquées dépassant le cadre de ce chapitre).

Le connecteur binaire d'égalité entre booléens est noté ⇔ et appelé équivalence : A ⇔ B se lit «A équivaut à B».

Negation

Le seul connecteur unaire utile est la negation ¬, qui échange les booléens (¬A se lit «non A»):
¬1
¬0
¬(¬A) 		⇔ 0
⇔ 1
⇔ A
Il est souvent noté en barrant le symbole principal de son argument, formant avec lui un autre symbole de même format:
x ≠ y
x ∉ E
(A ⇎ B)
 ⇔ ¬(x=y)
⇔ ¬(x ∈ E)
⇔ (A ⇔ ¬B)
 (x est différent de y)
(x n'appartient pas à E)
(Non-équivalence)

Conjonctions, disjonctions

La conjonction ∧ signifie «et», donnant vrai uniquement si ses deux arguments sont vrais;
La disjonction ∨ signifie «ou», donnant vrai sauf si ses deux arguments sont faux.
Chacun est:
Idempotent
(A ∧ A) ⇔ A
(A ∨ A) ⇔ A
 Commutatif
(B∧A) ⇔ (A∧B)
(B∨A) ⇔ (A∨B)
Associatif
((A∧B)∧C) ⇔ (A∧(B∧C))
((A∨B)∨C) ⇔ (A∨(B∨C))
 Distributif sur l'autre
(A ∧ (B∨C)) ⇔ ((A∧B) ∨ (A∧C))
(A ∨ (B∧C)) ⇔ ((A∨B) ∧ (A∨C))

Cette ressemblance (symétrie) de leurs propriétés vient du fait qu'ils sont échangés par négation:

(A ∨ B) ⇎ (¬A ∧ ¬B)
(A ∧ B) ⇎ (¬A ∨ ¬B)

L'inéquivalence ⇎ est aussi appelée «ou exclusif» car (A ⇎ B) ⇔ ((A ∨ B) ∧ ¬(A ∧ B)).

Les chaines de conjonctions comme (A ∧ B ∧ C) abrègent toute formule avec plus de parenthèses comme ((A ∧ B) ∧ C), équivalentes entre elles par associativité; de même pour les chaines de disjonctions (A ∨ B ∨ C).

Affirmer (déclarer vraie) une conjonction de formules revient à affirmer successivement toutes ces formules.

Implication

Le connecteur binaire d'implication ⇒ se definit par (A ⇒ B) ⇔ ((¬A) ∨ B). Il peut se lire «A implique B», «A est une condition suffisante à B», ou «B est une condition nécessaire à A». Etant vrai sauf quand A est vrai et B est faux, il exprime la vérité de B quand A est vrai, mais il ne donne plus d'information sur B quand A est faux (étant alors vrai).
De plus,
(A ⇒ B) ⇎
(A ⇒ B) ⇔		 (A ∧ ¬B)
(¬B ⇒ ¬A)
La formule (¬B ⇒ ¬A) est appelée la contraposée de (A ⇒ B).
L'équivalence peut aussi se redéfinir par
(A ⇔ B) ⇔ ((A ⇒ B) ∧ (B ⇒ A)).
Ainsi dans une théorie donnée, une preuve de A ⇔ B peut se former d'une preuve de la première implication (A ⇒ B), puis une preuve de la deuxième (B ⇒ A) appelée la réciproque de (A ⇒ B).

La formule (A ∧ (A ⇒ B)) sera abrégée en A ∴ B, qui se lit «A donc B». Elle est équivalente à (A ∧ B), mais sert à indiquer qu'elle est déduite des vérités de A et de (A ⇒ B).

Les négations transforment les formules d'associativité et de distributivité des conjonctions et disjonctions en diverses tautologies avec des implications:

(A ⇒ (B ⇒ C)) ⇔ ((A ∧ B) ⇒ C)
(A ⇒ (B ∨ C)) ⇔ ((A ⇒ B) ∨ C)

(A ⇒ (B ∧ C)) ⇔ ((A ⇒ B) ∧ (A ⇒ C))
((A ∨ B) ⇒ C) ⇔ ((A ⇒ C) ∧ (B ⇒ C))
((A ⇒ B) ⇒ C) ⇔ ((A ∨ C) ∧ (B ⇒ C))
(A ∧ (B ⇒ C)) ⇔ ((A ⇒ B) ⇒ (A ∧ C))
Enfin on a
(A ⇒ B) ⇒ ((A∧C) ⇒ (B∧C))
(A ⇒ B) ⇒ ((A∨C) ⇒ (B∨C)).

Chaines d'implications et d'équivalences

Par une autre sorte d'abréviation, toute chaine de formules reliées par des ⇔ et/ou ⇒, abrégera la conjonction de toutes ces implications ou équivalences entre formules voisines:

(A ⇒ B ⇒ C) ⇔ ((A ⇒ B) ∧ (B ⇒ C)) ⇒ (A ⇒ C)
(A ⇔ B ⇔ C) ⇔ ((A ⇔ B) ∧ (B ⇔ C)) ⇒ (A ⇔ C)
0 ⇒ A ⇒ A ⇒ 1
(¬A) ⇔ (A ⇒ 0) ⇔ (A ⇔ 0)
(A ∧ 1) ⇔ A ⇔ (A ∨ 0) ⇔ (1 ⇒ A) ⇔ (A ⇔ 1)
(A ∧ B) ⇒ A ⇒ (A ∨ B)

1.7. Classes en théorie des ensembles

Pour toute théorie, une classe est un prédicat unaire A vu comme ensemble des objets où A est vrai, à savoir «la classe des x tels que A(x)».
Notamment en théorie des ensembles, tout ensemble E est synonyme de la classe des x tels que x ∈ E (définie par la formule x ∈ E, d'argument x et de paramètre E). Mais cela utilise deux interprétations différentes de la notion d'ensemble, qui doivent être distinguées comme suit.

Univers standard et méta-ensembles

Interpréter (insérer) la théorie des ensembles dans elle-même, nécessite d’articuler deux interprétations (modèles) de la théorie des ensembles, qui seront distingués en donnant le préfixe méta à l'interprétation dans le rôle de cadre. Outre les interprétations génériques, la théorie des ensembles a un type standard d'interprétations dans elle-même où chaque ensemble est interprété par la classe (méta-ensemble) de ses éléments (l'ensemble et le méta-ensemble des mêmes éléments sont alors égaux), et chaque fonction est interprétée par sa méta-fonction synonyme.
Ainsi, tout ensemble est une classe, tandis que toute classe est un méta-ensemble d'objets. Mais certains méta-ensembles d'objets ne sont pas des classes (n'étant définissables par aucune formule avec paramètres; donner des exemples serait paradoxal car cela signifierait définir quelque chose d'indéfinissable, mais 1.B introduit de telles possibilités); et certaines classes ne sont pas des ensembles, par exemple la classe des ensembles (voir le paradoxe de Russell en 1.8), ou l'univers (classe de tous les objets, définie par 1).

Classes d'admissibilité

La théorie des ensembles accepte tous les objets comme «éléments» pouvant appartenir à des ensembles et être opérés par des fonctions (pour éviter les divisions sans fin entre ensembles d'éléments, ensembles d'ensembles, de fonctions, ensembles mixtes...). Cela serait formalisable en gardant 3 types (éléments, ensembles et fonctions) où chaque ensemble aurait une copie comme élément, identifiée par un foncteur des ensembles vers les éléments, et de même pour les fonctions. Mais au-delà de ces types, notre théorie des ensembles aura de toute façon besoin d'autres notions comme domaines de ses structures, qui ne peuvent être commodément formalisées que comme classes. Alors gardons "élément" comme type unique contenant tous les objets, et formalisons les notions d'ensemble et de fonction comme classes désignées par des symboles de prédicats:

Set = «est un ensemble»
Fnc = «est une fonction»

En logique du premier ordre, toute expression est assurée de prendre une valeur définie, pour chaque donnée d'un modèle et de valeurs de ses variables libres dedans (en raison de sa correction syntaxique implicite dans le concept d '«expression»). Mais en théorie des ensembles, cela peut encore dépendre des valeurs des variables libres.
Ainsi une expression A (et toute structure qu'elle définit) sera dite admissible si elle a effectivement une valeur pour les valeurs données de ses variables libres (vues comme arguments et paramètres de toute structure qu'elle définit). Cette condition est elle-même un prédicat partout admissible, exprimé par une formule dA avec les mêmes variables libres. En choisissant une d'elles comme argument, la classe qu'elle définit est le méta-domaine, appelé classe d'admissibilité, de la structure unaire définie par A.
Les expressions ne doivent être employées que là où elles sont admissibles, ce qui se fera assez naturellement. La condition d'admissibilité de (x ∈ E) est Set(E). Celle de l'évaluateur de fonction f(x), est (Fnc(f) ∧ x ∈ Dom f).
Mais l'admissibilité de cette dernière formule nécessite une justification, donnée plus bas.

Admissibilité étendue

Une théorie aux structures partiellement admissibles, comme la théorie des ensembles, peut être formalisée (traduite) en théorie avec un seul type et des structures partout admissibles, gardant intactes les expressions et leurs valeurs partout où elles sont admissibles : les modèles se traduisent dans un sens en donnant des valeurs arbitraires aux structures non admissibles (par exemple une valeur constante), et en sens inverse en ignorant ces valeurs. Ainsi, une expression comportant une sous-expression non admissible peut être déclarée admissible si sa valeur finale ne dépend pas de ces valeurs ajoutées.
En particulier, pour toutes formules A et B on considèrera les formules A ∧ B et A ⇒ B comme admissibles si A est faux, de valeurs respectives 0 et 1, même si B n'est pas admissible. Donnons leur ainsi la même condition d'admissibilité (dA ∧ (A ⇒ dB)) (rompant, pour «et», la symétrie entre A et B qu'il est inutile de rétablir). Cette formule est rendue admissible par la même règle dès lors que dA et dB étaient admissibles. Ainsi les deux formules

A ∧ (B ∧ C)
(A ∧ B) ∧ C

ont la même condition d'admissibilité (dA ∧ (A ⇒ (dB ∧ (B ⇒ dC)))).

Les classes seront définies par des prédicats unaires partout admissibles, facilement exprimables par la règle ci-dessus comme suit.
Tout prédicat A peut être étendu au-delà de son domaine d'admissibilité, sous la forme dA ∧ A (donnant 0) ou dA ⇒ A (donnant 1).
Pour toute classe A et tout prédicat unaire B admissible sur tout A, la classe définie par A∧B est appelée la sous-classe de A définie par B.

1.8. Symboles liants en théorie des ensembles

Syntaxe des symboles liants

Cette dernière sorte de symbole peut former une expression en prenant un symbole de variable, disons ici x, et une expression F pouvant utiliser x comme variable libre (en plus des variables libres disponibles à l’extérieur), pour donner une valeur dépendant de la structure unaire définie par F d'argument x. Ainsi, il sépare la sous-expression «intérieure» F ayant x parmi ses variables libres, de l'«extérieur» où x est liée. Mais dans la plupart des cas (la plupart des théories...), les symboles liants ne peuvent pas conserver la donnée complète de cette structure unaire, trop complexe pour être enregistrée comme objet, comme expliqué ci-dessous.

Nous présenterons d’abord les deux principaux symboles liants en théorie des ensembles: le symbole de compréhension et le définisseur de fonctions. Puis, 1.9 présentera les deux principaux quantificateurs. Enfin 1.10 et 1.11 donnera des axiomes complétant cette formalisation des notions d’ensemble et de fonction en théorie des ensembles.

La syntaxe diffère entre la logique du premier ordre et la théorie des ensembles, qui gèrent le domaine des variables différemment. En logique du premier ordre, les domaines sont des types, données implicites des quantificateurs. Mais les domaines des symboles liants en théorie des ensembles sont des ensembles qui, comme objets, sont désignés par un argument supplémentaire du symbole (un espace pour un terme n'utilisant pas la variable à lier).

Symbole de compréhension

Pour tout prédicat unaire A admissible dans un ensemble E, la sous-classe de E définie par A est un ensemble: c'est le domaine d'une variable x introduite comme parcourant E, donc liable, dont on sélectionne les valeurs satisfaisant A(x). C'est donc un sous-ensemble ou une partie de E, noté {x∈E | A(x)} (ensemble des x dans E tels que A(x)): pour tout y,

y ∈ {x ∈ E|A(x)} ⇔ (y ∈ E ∧ A(y))

Cette combinaison de caractères { ∈  |  } forme la notation d'un symbole liant appelé symbole de compréhension : {x∈E | A(x)} lie x de domaine E sur la formule A.

Paradoxe de Russell

Si l'univers (classe de tous les éléments) était un ensemble alors en l'utilisant, le symbole de compréhension pourrait convertir en ensembles toutes les classes, dont la classe de tous les ensembles. Mais c'est impossible, comme on peut montrer à l'aide du symbole de compréhension lui-même :

Théorème. Pour tout ensemble E il existe un ensemble F tel que F ∉ E. Ainsi aucun ensemble E ne peut contenir tous les ensembles.

Preuve. F = {x∈E | Set(x) ∧ x ∉ x} ⇒ (F ∈ F ⇔ (F ∈ E ∧ F ∉ F)) ⇒ (F ∉ F ∧ F ∉ E). ∎

Cela nous obligera à préserver les distinctions entre ensembles et classes.

Définitions des fonctions par des termes

Le définisseur de fonction (  ∋   ↦  ) lie une variable sur un terme, suivant la syntaxe (E ∋ x ↦ t(x)) où Admissible si t(x) est admissible pour tout x dans E, il prend alors le foncteur défini par t et restreint son domaine (classe d'admissibilité) à E, pour donner une fonction de domaine E.
Il convertit donc les foncteurs en fonctions, à l'inverse du rôle de l'évaluateur de fonction (avec le foncteur Dom) qui convertissait (interprétait) les fonctions en leur rôle (signification) comme foncteurs dont les classes d'admissibilité étaient des ensembles.
La notation abrégée x ↦ t(x) peut être utilisée lorsque E est déterminé par le contexte, ou dans une méta-description pour désigner un foncteur en spécifiant l'argument x du terme qui le définit.

Relations

Une relation est un objet de la théorie des ensembles semblable à une opération mais à valeurs booléennes: il joue un rôle de prédicat dont les classes d'admissibilité (domaines des arguments) sont des ensembles (les prédicats peuvent ainsi se décrire comme relations entre types interprétés).

Les relations unaires (fonctions à valeurs booléennes), seront représentées par des sous-ensembles S de leur domaine E, en utilisant le symbole de compréhension comme définisseur, et ∈ comme évaluateur interprétant S comme prédicat x ↦ (x ∈ S). Ce rôle de S diffère encore de la relation unaire voulue, ignorant son domaine E, mais étant admissible dans tout l'univers, valant 0 hors de E. Cette absence d'opérateur Dom n'a pas d'importance, E étant généralement connu par le contexte (comme variable disponible).

Comme le définisseur de fonction (resp. le symbole de compréhension) enregistre toute la structure définie par l'expression donnée sur l'ensemble donné, il suffit à définir tout autre symbole liant ensembliste de même domaine sur la même expression, comme composé d'une structure unaire appliquée à son résultat (qui est une fonction, resp. un ensemble).

1.9. Axiomes et preuves

Enoncés

Une expression est close, si sa liste de variables libres est vide (toutes ses variables sont liées), de sorte que sa valeur ne dépend que du système où elle est interprétée.
En logique du premier ordre, un énoncé est une formule close. Un énoncé A aura donc une valeur booléenne précise (vrai ou faux) dépendant uniquement du choix d'un système M interprétant son langage. On note M⊨A la véracité de A dans M.
La liste des axiomes d'une théorie est un ensemble d'énoncés, présentés comme tous vrais dans certains systèmes donnés appelés modèles de la théorie. Expliquons.

Théories réalistes vs axiomatiques en mathématiques et autres sciences

Après la distinction de nature (mathématique ou non), les théories peuvent également différer selon l'intention de leur usage, entre réalisme et formalisme :

Une théorie axiomatique est une théorie formellement donnée T = (τ, L, X) avec une liste X d'axiomes visant à définir la classe de ses modèles, comme celle de tous les systèmes M interprétant le langage L où tous les axiomes (éléments de X) sont vrais, ce qu'on notera M⊨T.

Une théorie réaliste est une théorie invoquée pour décrire soit un système fixe soit un système variable (une classe de systèmes), vus comme donnés par une réalité indépendante. Ses axiomes donnés sont des énoncés qui, pour certaines raisons, sont considérés connus comme vrais sur ces systèmes. Une telle théorie est "vraie" si tous ses axiomes y sont effectivement vrais. Ces systèmes sont alors des modèles, qualifiés de standard par contraste avec les autres modèles (non voulus) de cette théorie prise axiomatiquement.

Cette véracité sera habituellement assurée pour les théories réalistes des mathématiques pures : arithmétique et théorie des ensembles (bien que la signification réaliste de la théorie des ensembles ne soit pas toujours claire suivant les axiomes considérés). Ces théories admettront également des modèles non standard, rendant effective la différence entre leurs significations réaliste et axiomatique.
Hors des mathématiques pures, la véracité des théories réalistes peut être douteuse (discutable): les énoncés non mathématiques sur des systèmes non mathématiques peuvent être ambigus (mal définis), tandis que la vérité des théories des mathématiques appliquées peut être approximative, ou spéculative comme les systèmes "réels" voulus peuvent être inconnus (contingents parmi d'autres systèmes possibles). Une telle théorie est dite falsifiable si en principe, le cas de sa fausseté peut être découvert en comparant ses prédictions (théorèmes) avec les observations.
Par exemple, la biologie est relative à un grand nombre de choix aléatoires discrètement accumulées par la nature sur Terre pendant des milliards d'années. Elle contient de nombreux "axiomes", falsifiables et qui nécessitent de nombreux tests empiriques.
Les théories non-réalistes en dehors des mathématiques (non qualifiées d'axiomatiques par manque de précision mathématique) seraient des œuvres de fiction décrivant des systèmes imaginaires ou futurs possibles.

La géométrie euclidienne fut d'abord conçue comme théorie réaliste de mathématiques appliquées (pour son rôle de première théorie physique), puis fut comprise comme une théorie axiomatique de mathématiques pures parmi d'autres géométries également légitimes mathématiquement ; tandis que l'espace physique réel est plus précisément décrit par la géométrie non-euclidienne de la Relativité Générale.

Démontrabilité

Une preuve ou démonstration d'un énoncé A dans une théorie T, est un modèle fini d'une théorie de la démonstration (réduite à la description d'une unique preuve), présentant A en "conclusion" et utilisant une liste finie d'axiomes parmi ceux de T.
Des formalisations complètes appropriées du concept de preuve pour la logique du premier ordre ont pu être établies par les spécialistes. Elles peuvent prendre la forme de théories de la démonstration formalisées (comme théories axiomatiques), ou d'algorithmes de vérification de preuves (n'utilisant qu'une quantité de ressources de calcul liée à la taille d'une preuve donnée).
Mais la plupart des travaux mathématiques ne sont que partiellement formalisés: on utilise des preuves semi-formelles, juste assez rigoureuses pour donner l’impression qu’une formalisation complète est possible sans l'avoir en fait rédigée; une vision intuitive d'un problème peut sembler plus claire qu'un raisonnement formel. De même, ce travail présentera des preuves naturellement sans formalisation complète explicite : utilisant parfois des articulations en langage courant, elles seront principalement écrites sous forme d’une succession d’énoncés, chacun visiblement vrai en vertu des précédents, de prémisses, d'axiomes, de théorèmes connus, et de règles de preuve, notamment celles des quantificateurs (1.10). Les fins de preuves sont marquées par "∎".
Mais sans détailler une théorie de la démonstration, voyons-en quelques propriétés générales.

On dit que A est démontrable (ou ) dans T, ou un théorème de T, et on note T ⊢ A s'il existe une preuve de A dans T. En pratique, seuls sont qualifiés de théorèmes les énoncés connus comme tels, à savoir dont on connait une preuve. Mais des synonymes de "théorème" sont traditionnellement utilisés pour les qualifier suivant leur importance: un théorème est plus important qu'une proposition. L'un ou l'autre peuvent se déduire d'un lemme autrement moins important, et implique facilement un corolaire aussi moins important.

Toute bonne théorie de la démonstration doit bien entendu être correcte, à savoir qu'elle ne peut "prouver" que des énoncés toujours vrais: la démontrabilité implique la vérité dans chaque modèle (où tous les axiomes sont vrais).

Validité logique

Pour un langage donné L, un énoncé A est dit logiquement valide, s'il est démontrable avec L sans utiliser d'axiome. On pourrait noter cela ⊢ A mais par mesure d'exactitude il faut l'écrire L ⊢ A (signifiant que A est théorème de la théorie faite de L sans axiome, donc de toute autre théorie contenant L), Alors, A est vrai dans tous les systèmes interprétant L en vertu du caractère correct du cadre logique.
Les plus simples énoncés logiquement valides sont les tautologies (dont les variables Booléennes sont remplacées par des énoncés); d'autres seront donnés en 1.10.

Une preuve de A utilisant certains axiomes peut se voir comme une preuve de (conjonction de ces axiomes ⇒ A) sans axiome, rendant cette implication logiquement valide.

Réfutabilité et cohérence

Une réfutation de A dans T, est une preuve de ¬A. S'il en existe (T ⊢ ¬A), l'énoncé A est dit réfutable (dans T).
Un énoncé est dit décidable (dans T) s'il est démontrable ou réfutable.
Une contradiction d'une théorie T est une preuve de 0 dans T. S'il en existe (T ⊢ 0), la théorie T est dite contradictoire ou inconsistante. Sinon est est dite cohérente.
Une réfutation de A dans T peut se voir comme une contradiction de la théorie T∧A obtenue en ajoutant A aux axiomes de T.
Si un énoncé est à la fois démontrable et réfutable dans T alors tous le sont, car cela signifie que la théorie est contradictoire, indépendamment de l'énoncé choisi :

⊢ (A ∧ ¬A) ⇔ 0
((T ⊢ A) ∧ (T ⊢ B)) ⇔ (T ⊢ A∧B)
((T ⊢ A) ∧ (T ⊢ ¬A)) ⇔ (T ⊢ 0).

Ainsi une contradiction peut être présentée comme une preuve de A avec une réfutation de A. Dans une théorie contradictoire, tout énoncé est démontrable. Son cadre étant correct, une telle théorie n'a aucun modèle.

Au-delà de la qualité indispensable de correction de la partie théorie de la démonstration d'un cadre logique, plus remarquable est sa qualité réciproque de complétude: pour toute théorie axiomatique qu'il décrit, tout énoncé vrai dans tous les modèles est démontrable. Autrement dit, tout énoncé non démontable est faux quelque part et tout énoncé irréfutable est vrai quelque part. Ainsi, toute théorie cohérente a des modèles existants, mais souvent une diversité de ceux-ci, car tout énoncé indécidable est vrai dans certains et faux dans d'autres. Ajouter des énoncés indécidables aux axiomes conduit à différentes théories cohérentes pouvant être «en désaccord» sans conflit, descriptions correctes de systèmes différents qui existent également. Cela résout le gros des divergences a priori entre Platonisme et formalisme, tout en donnant un sens clair et naturel aux concepts a priori intuitifs de «démonstration», «théorème» et «cohérence».

1.10. Quantificateurs

Un quantificateur est un symbole liant exercé sur un prédicat unaire (une formule) et à valeurs booléennes.

Quantificateurs bornés; quantificateurs ouverts

Un quantificateur Q est dit borné lorsqu'il suit le fornat d'usage ensembliste des symboles liants (1.8) : son domaine est un ensemble donné en argument. Pour les quantificateurs ce format se note (Q ∈ , ) rempli comme (Qx∈E, A(x)) pour prendre en entrée un prédicat unaire A, en liant une variable x de domaine E sur une quelconque formule ici abrégée en A(x) pour signifier qu'elle définit A d'argument x avec d'éventuels paramètres.
Primitivement en logique du premier ordre, les domaines des quantificateurs sont des types (le même type que la variable liée, formellement pas un argument). Tout domaine E (type, classe ou ensemble) peut être marqué en indice (QEx, A(x)), ou supprimé (Qx,A(x)) quand il est sans importance, ou sous-entendu comme fixé par le contexte.
Lorsque la théorie des ensembles est formalisée en logique du premier ordre, les quantificateurs de la logique du premier ordre, parcourant l'univers, et leurs variantes parcourant des classes (définis à partir d'eux ci-dessous), sont appelés des quantificateurs ouverts par opposition au cas restreint des quantificateurs bornés (comme les ensembles sont des cas particuliers de classes). Dans ce contexte, une formule est dite bornée si tous ses quantificateurs sont bornés. Cette condition sera requise pour certaines utilisations (1.A, 1.C, 2.1, 2.2).

Les deux principaux quantificateurs

Les deux principaux quantificateurs (par lesquels d'autres seront définis en 2.6) sont: Le quantificateur universel borné est définissable par le symbole de compréhension :

(∀x∈E, A(x)) ⇔ {x∈E | A(x)} = E.

Les quantificateurs de tout domaine peuvent se définir dans des interprétations ensemblistes en regardant A comme une fonction, et ses valeurs booléennes comme des objets:

(∀x, A(x)) ⇔ A = (x ↦ 1)
(∃x, A(x)) ⇔ A ≠ (x ↦ 0)
(∃x, A(x)) ⇎ (∀x, ¬A(x))

La formule (∀x,1) est toujours vraie. Les quantificateurs sur les classes peuvent se définir par

(∀C x, A(x)) ⇔ (∀x, C(x) ⇒ A(x))
(∃C x, A(x)) ⇔ (∃x, C(x) ∧ A(x)) ⇔ ∃C∧A x, 1

Inversement, toute classe est définissable à partir d'un quantificateur sur elle: ∀x, (C(x) ⇔ ∃C y, x=y).

Inclusion entre classes

Une classe A est dite incluse dans une classe B si ∀x, A(x) ⇒ B(x). Alors A est une sous-classe de B car ∀x, A(x) ⇔ (B(x) ∧ A(x)). Réciproquement, toute sous-classe de B est incluse dans B.
L'inclusion de A dans B entraîne pour tout prédicat C (en cas d'admissibilité):

(∀B x, C(x)) ⇒ (∀A x, C(x))
(∃A x, C(x)) ⇒ (∃B x, C(x))
(∃C x, A(x)) ⇒ (∃C x, B(x))
(∀C x, A(x)) ⇒ (∀C x, B(x))

Règles de preuves pour les quantificateurs sur un prédicat unaire

Tout comme les expressions furent décrites en permettant de prendre des expressions déjà faites pour en former de nouvelles, on peut formaliser le concept de preuve en utilisant des preuves déjà connues pour en former de nouvelles. Voici quelques règles intuitivement introduites, sans prétention de formalisation complète.

Introduction existentielle. Si on a des termes t, t′,… et une preuve de (A(t) ∨ A(t′) ∨ …), alors ∃x,A(x).

Elimination existentielle. Si ∃x, A(x), alors on peut introduire une nouvelle variable libre z avec l'hypothèse A(z) (les conséquences seront justes, sans restreindre la généralité).

Ces règles traduisent le sens de ∃ : le passage de t, … à ∃ puis de ∃ à z, revient à abréger par z un des termes t, … (sans savoir lequel mais ils pourront être rassemblés en un seul par l'opérateur conditionnel). Elles donnent le même sens à ∃C qu'à ses 2 formules équivalentes ci-dessus, court-circuitant (rendant implicite) la règle d'admissibilité étendue de (C ∧ A) en se concentrant sur le cas où C(x) est vrai et donc A(x) est admissible.

Alors que ∃ apparaissait comme désignation d'objet, ∀ se présente comme une règle de déduction: ∀C x, A(x) signifie que sa négation ∃C x, ¬A(x) entraine une contradiction.

Introduction universelle. Si de la seule hypothèse C(x) sur une nouvelle variable libre x on a pu déduire A(x), alors ∀C x, A(x).

Elimination universelle. Si ∀C x, A(x) et t est un terme satisfaisant C(t), alors A(t).

Introduire puis éliminer ∀ revient à remplaçer x par t dans la démonstration initiale.

Formules logiquement valides

Ces règles permettent d'établir les formules logiquement valides suivantes

((∀C x, A(x)) ∧ (∀C x, A(x) ⇒ B(x))) ⇒ (∀C x, B(x))
((∃C x, A(x)) ∧ (∀C x, A(x) ⇒ B(x))) ⇒ (∃C x, B(x))
((∀C x, A(x)) ∧ (∃C x, B(x))) ⇒ (∃C x, A(x) ∧ B(x))
(∀C x, A(x)∨B(x)) ⇒ ((∀C x, A(x)) ∨ (∃C x, B(x)))
(∀A x, ∀B y, R(x,y)) ⇔ (∀B y, ∀A x, R(x,y))
(∃A x, ∃B y, R(x,y)) ⇔ (∃B y, ∃A x, R(x,y))
(∃A x, ∀B y, R(x,y)) ⇒ (∀B y, ∃A x, R(x,y))
∀x, (∀y, R(x,y)) ⇒ R(x,x) ⇒ (∃y, R(x,y))

On utilisera les abréviations suivantes, et de même pour les quantificateurs bornés: La validité logique dépend du langage parce que, avec un seul type

(L ⊢ ∃x, 1) ⇔ (un symbole de constante existe dans L)

(Avec plus de types, la condition est plus compliquée ; mais comme la plupart des théories utiles exigent que tous les types soient non vides, la dépendance au langage peut être ignorée en pratique)

Complétude de la logique du premier ordre

La logique du premier ordre a été trouvée complète, ce qu'exprime le théorème de complétude, qui était à l’origine la thèse de Gödel: à partir d’un concept de «démonstration» convenablement formalisé, la classe résultante de théorèmes (potentiels) de toute théorie du premier ordre se trouve être celle "parfaite", équivalente à la véracité universelle (classe des énoncé vrais dans tous les modèles M):

∀A, (T ⊢ A) ⇔ (∀M, (M⊨T)⇒(M⊨A))

Une telle théorie de la démonstration pour la logique du premier ordre est essentiellement unique: l'équivalence entre deux versions (correctes et complètes) concernant l'existence d'une preuve d'un énoncé dans une théorie, apparaît concrètement par la possibilité de traduire toute "preuve" pour l'une en une "preuve" pour l'autre.

Cette qualité de la logique du premier ordre confirme son importance centrale dans les fondements des mathématiques, après sa capacité à exprimer toutes les mathématiques : tout cadre logique peut de toute façon être développé en théorie des ensembles (ou plus directement ses théories peuvent être interprétées en théorie des ensembles) elle-même exprimable comme théorie du premier ordre.

La preuve du théorème de complétude, qui nécessite l'axiome de l'infini (l'existence de ℕ) consistera à construire un modèle de toute théorie axiomatique cohérente du premier ordre, comme suit (détails en 4.7). L'ensemble (infini) de toutes les termes clos dont les symboles d'opérateur dérivent de la théorie (ceux de son langage plus d'autres issus de ses axiomes existentiels) devient un modèle en définissant progressivement chaque symbole de prédicat sur chaque combinaison de valeurs de ses arguments, par une règle conçue pour maintenir la cohérence.

Cette construction est non algorithmique: elle nécessite une infinité d'étapes, dont chacune dépend d'une connaissance infinie (à savoir si le prédicat donné sur des arguments donnés, vu comme un axiome supplémentaire candidat, préserve la cohérence avec ceux précédemment acceptés). En fait, la plupart des théories fondatrices, telles que les théories des ensembles, n’ont aucun modèle définissable par un algorithme.

1.11. Quantificateurs universels du second ordre

La logique du premier ordre peut être développée pour autoriser l'utilisation de symboles de structures variables comme abréviations d'expressions fixes définissant ces structures avec paramètres variables, mais ainsi ne peut les lier que sur des domaines restreints dépendant des expressions choisies (plus de commentaires en 1.D).
Appelons quantificateur du second ordre, un quantificateur liant un symbole de structure variable sur l'ensemble de toutes les structures de son type de symbole. Ceci peut être conçu soit comme l'ensemble de toutes les expressions définissables (par toutes les expressions avec n'importe quel nombre de paramètres), soit comme l'ensemble complet de toutes ces opérations (reliant les types interprétés donnés) qui existent... dans l'univers. Utiliser des quantificateurs du second ordre signifie travailler dans un cadre logique élargi, notamment une version de la logique de second ordre (décrite dans la partie 5), suivant les détails.

Comme on fera pour les axiomes de l’égalité (ci-dessous) puis pour la théorie des ensembles (en 2.1 et 2.2), une théorie peut être d’abord exprimée en logique du second ordre pour des raisons intuitives, avant d’interpréter cela formellement comme un outil commode de niveau méta pour abréger une formalisation du premier ordre, comme suit.

Soit T une théorie du premier ordre, T' son extension par un symbole de structure s (sans axiome supplémentaire) et F un énoncé de T' (en logique du premier ordre) également noté F(s) lorsque vu comme une formule de T utilisant le symbole de structure variable s en logique du second ordre.

Introduction universelle de second ordre. Si T'⊢F alors T implique l'énoncé du second ordre (∀s, F(s)).

Ceci est valable pour tout modèle et le domaine ensembliste complet de s, indépendamment de l'univers dans lequel les modèles et les structures s sont recherchés.

Élimination universelle de second ordre. Une fois accepté un énoncé de second ordre (∀s, F(s)) dans une théorie T, il se manifeste en logique du premier ordre sous la forme d'un schéma d'énoncés (axiomes ou théorèmes), c'est-à-dire une liste infinie d'énoncés de la forme (∀parameters, F(s)) pour chaque remplacement possible de s par une expression définissante avec des paramètres.

Appliquer l’élimination universelle de second ordre après l’introduction universelle de second ordre signifie déduire de T un schéma de théorèmes, chacun déductible en logique du premier ordre en remplaçant s par sa définition respective dans la preuve originale.

Incomplétude de la logique du second ordre

Les règles de preuve ci-dessus, qui suffiront à nos besoins, sont clairement correctes, mais contrairement à la logique du premier ordre, la logique du second ordre n'admet aucune théorie de la démonstration correcte et complète. Dans ce qui précède, la seule règle de preuve complète est que l'élimination universelle de second ordre formalise complètement les conséquences de ∀ entendu comme portant sur les seules structures définissables. Aucune règle ne peut épuiser les conséquences de l'application de ∀ au domaine de "toutes les structures" (y compris celles indéfinissables) pour la raison suivante dont les détails seront développés ultérieurement.

Une théorie est dite complète si elle détermine essentiellement son modèle. La définition exacte est que tous les modèles sont isomorphes entre eux (3.3); retenons-en qu'elle détermine toutes les propriétés de son modèle (valeurs des énoncés du premier ordre) et exclut les modèles non standard.
L'arithmétique (la théorie décrivant le système ℕ des entiers naturels avec quatre symboles 0, 1, +, ⋅) peut être formalisée comme théorie complète en logique du second ordre (axiomes listés en 4.4 et 4.5). La seule composante de cette formalisation au-delà de la logique du premier ordre est l'axiome d'induction, utilisant un ∀ s'étendant sur "tous les prédicats unaires" (y compris ceux indéfinissables). Cependant, le théorème d'incomplétude (1.C) réfutera la possibilité pour tout algorithme de donner les valeurs correctes de tous les énoncés arithmétiques du premier ordre.

Mais l'ensemble des seules structures définissables d'un type donné ne peut pas non plus être complètement défini pour la même raison, car décrire l'ensemble infini exact de toutes les expressions de définitions possibles revient à décrire ℕ.

Axiomes de l'égalité

En logique du premier ordre avec des types et un langage donnés, certains énoncés utilisant = sont valides (toujours vrais) pour le domaine d'interprétations conservant = en tant que prédicat = de la théorie des ensembles, mais non plus pour le domaine plus large d'interprétations l'interprétant comme tout autre prédicat. Une liste possible d'axiomes de l'égalité est une liste de certains de ces énoncés qui suffisent à impliquer tous les autres dans ce contexte.
Une de ces listes comprend les 2 axiomes suivants par type, le dernier étant à lire comme un schéma d'axiomes par élimination universelle de second ordre du prédicat unaire variable A:
  1. ∀x, x = x (réflexivité)
  2. ∀A,∀x,y, (x = y ∧ A(y)) ⇒ A(x).
Les variables x et y peuvent également servir parmi les paramètres de la définition de A. Ceci peut être compris en réordonnant les quantificateurs en (∀x, ∀y, ∀A), ou comme déduit de l'usage d'un A de paramètres a, b, en adaptant un énoncé logiquement valide de 1.10 :

∀a,b, (∀x,y, R(a, b, x,y)) ⇒ R(a, b, a,b)

Diverses définitions de A donnent divers énoncés (en supposant la réflexivité):

Enoncé
3. ∀x,y, x = y ⇒ y = x
4. ∀x,y,z, (x = y ∧ y = z) ⇒ x = z
5. ∀f, ∀x,y, x = y ⇒ f(x) = f(y)
6. ∀A, ∀x,y, x = y ⇒ (A(x) ⇔ A(y))
7. ∀x,y,z, (x = y ∧ z = y) ⇒ z = x		 Qualité de =
Symétrique
Transitive


Euclidienne à gauche 		A(u) utilisé
y = u
u = z
f(u) = f(y)
¬A(u)
z = u

5. est un schéma d'énoncés avec f parcourant les foncteurs entre deux types quelconques.
6. peut aussi se déduire par symétrie.

Remarque. (1.∧7.) ⇒ 3., puis 3. ⇒ (4. ⇔ 7) donc (1.∧7.) ⇔ (1.∧3.∧4.).
La formule (x = y ∧ y = z) sera abrégée en x = y = z.

Une autre liste possible d'axiomes de l'égalité consiste en les énoncés 1. à 5. où f et A parcourent les seuls symboles du langage, pris chacun une fois par argument: le schéma complet de 2. est impliqué par déductions successives pour chaque occurrence de symbole dans A. Ceci sera plus précisément justifié en 2.11 (relations d’équivalence).

Définir de nouveaux symboles liants

Un nouveau symbole de variable libre x défini par un terme t peut être introduit, soit déclarée par une ligne de preuve distincte (x = t) servant d'axiome, soit dans une ligne comme (x = t ⇒ ...). On peut le justifier par les règles comme

(∀x, x = x) ∴ t = t ∴ ∃x, (x = t ∴ ...).

En liant un paramètre, la définition d'un symbole de foncteur f par un terme ici abrégé t de variable x (qui justifiera la notation abrégée de t comme symbole de foncteur), est déclarée par l'axiome

∀x, f(x) = t(x).

De même, les symboles d'opérateur peuvent être définis en liant plusieurs paramètres, et les classes et autres prédicats peuvent être définis de même en remplaçant = par ⇔.
Enfin, un nouveau symbole liant B utilisable dans une théorie du premier ordre T (à savoir en théorie des ensembles formalisée avec sa traduction en théorie du premier ordre) peut être défini par une expression ici abrégée par F(A) car utilisant, au-delà du langage de T, un symbole A de structure unaire variable (dont l'argument sera lié par B). Une telle définition peut être déclarée par cet axiome de second ordre:

∀A, (Bx, A(x)) = F(A)

où = devient ⇔ si les valeurs sont booléennes. Par élimination universelle du second ordre, cela donne un schéma de définitions en logique du premier ordre: pour chaque expression définissant A, l'expression (Bx, A(x)) se définit comme un symbole de structure, par l'expression définissant F(A), obtenue en remplaçant A par sa définition dans l'expression F. Ses variables libres disponibles sont donc les paramètres de F plus ceux de A.

Aspects philosophiques des fondements des mathématiques

Complétons notre initiation aux fondements des mathématiques, par des aspects plus philosophiques: comment la réalité mathématique est structurée par un flux de son propre "temps" de type "bloc en croissance" indépendant de notre temps. Ces compléments ne sont pas nécessaires pour continuer avec la partie 2 (2.1 à 2.10 sauf petites remarques en 2.2, 2.7 et 2.10), partie 3 et plus, tandis que 2.A-2.C requiert à la fois la partie 1 jusqu'à 1.D et la partie 2 jusqu'à 2.7.

1.A. Temps en théorie des modèles

L'ordre temporel de l'interprétation des expressions

Les interprétations des expressions d'une théorie T dans un modèle M dépendent les unes des autres, donc viennent comme calculées les unes après les autres. Cet ordre temporel suit l'ordre de construction des sous-expressions vers les expressions qui les contiennent.
Par exemple, pour donner un sens à la formule xy + x = 3, les variables libres x et y doivent prendre une valeur en premier. Puis, xy prend une valeur, obtenue en les multipliant. De là, xy+x prend une valeur, puis la formule entière (xy+x=3) prend une valeur booléenne dépendant des valeurs de x et y. Enfin, en prenant par exemple la formule close ∀x, ∃y, xy+x=3, sa valeur booléenne (qui est faux dans le monde des nombres réels), «est calculée à partir de» celles prises par la formule précédente pour toutes les valeurs possibles de x and y, et vient donc après elles.

Les interprétations d'une liste finie d'expressions peuvent être rassemblées par une seule autre expression, les prenant comme sous-expressions. Cette grande expression est interprétée après elles toutes, mais appartient toujours à la même théorie.
Mais pour qu'une même expression invoque un ensemble infini d'expressions (tel que l'ensemble de toutes les expressions de T, ou seulement tous les termes ou tous les énoncés), ces expressions doivent être traitées comme objets (valeurs d'une variable). Si T est une théorie fondatrice, elle peut définir (ou construire) un système ressemblant à ceci, de sorte que, dans tout modèle standard de T (en un sens qui sera précisé plus loin), cette définition désignera une copie exacte de cet ensemble d'expressions.

Cependant, l'interprétation systématique de toutes les expressions de T dans M ne peut correspondre à aucune définition par une seule expression de T interprétée dans le même M. À savoir, cela fait partie du système combiné [T,M] au-delà de M, décrit par une théorie du modèle (1MT) qui, même si elle peut être développée à partir de T, nécessite de toute façon une autre interprétation, à un niveau méta au-dessus de M.

Le temps infini entre les modèles

Sans chercher à formaliser la théorie du modèle MT de la logique du premier ordre (qui sera abordée dans les prochaines sections), esquissons une classification de ses composants (mélangeant notions, structures et axiomes) en parties selon ce qu'elles décrivent. La plupart des questions sont inchangées en restreignant la considération à un 1MT, de modèle un seul système [T,M] fait d'une théorie T avec un modèle M, lorsque ces T et M (spécifiables par un choix de variante de 1MT) sont assez grands pour essentiellement contenir toute théorie et tout système. La dernière partie de [T,M] est une construction mathématique déterminée par la combinaison des deux systèmes T et M, mais n'est pas directement contenue dans ces données: elle est construit après.

La métaphore du temps usuel

Je peux parler de «ce que dont j'ai parlé à tel instant»: cela a bien un sens si ce propos passé en avait un, car j'en avais saisi le sens et je m'en souviens. Mais parler de «ce dont je parle» tout court, n'informerait pas sur ce dont il s'agit: cela pourrait être n'importe quoi, et devient absurde dans une phrase qui modifie ou contredit ce sens («le contraire de ce que je dis»). Parler de «ce dont je parlerai demain», même en sachant déjà ce que je dirai, ne suffirait pas non plus à en donner déjà le sens: au cas où je parlerai de «ce dont j'ai parlé hier» (donc maintenant) cela ferait un cercle vicieux; mais même si la forme de mon futur propos assurait que son sens existera demain, cela ne le donnerait pas encore aujourd'hui. Quelles que soient mes spéculations, le sens réel des expressions qui seront prononcées ne surviendra qu'en leur temps, dans le contexte à venir.
Faute d'intérêt à décrire des expressions sans leur signification, autant restreindre l'étude aux propos passés, se contenter de "vivre" les propos présents et ignorer ceux à venir. Ainsi, mon actuel univers du passé que je peux décrire aujourd'hui, inclut celui d'hier, mais aussi mes propos d'hier sur celui-ci et leur signification. Je peux donc décrire aujourd'hui des choses extérieures à l'univers que je pouvais décrire hier. Or, depuis hier, je n'ai pas appris à parler le Martien ni n'ai acquis une nouvelle intelligence transcendantale; mais le même langage s'applique à un univers plus vaste, enrichi de nouveaux objets. Ces nouveaux objets étant de mêmes types que les précédents, mon univers d'aujourd'hui peut ressembler à celui d'hier; mais d'un univers à l'autre, les mêmes expressions peuvent prendre des sens différents.

Comme des historiens, chaque théorie mathématique ne peut «à chaque instant donné» que décrire un système d'objets mathématiques passés. Son interprétation dans ce système, «se produit» formant un présent mathématique hors de ce domaine (au-delà de ce passé).
Puis décrire cet acte d'interprétation, c'est étendre la portée de nos descriptions: le modèle [T,M] de 1MT, englobant les interprétations de toutes les expressions de T dans le présent système M des objets passés, est le prochain domaine du passé, venant lorsque la totalité infinie des interprétations actuelles (dans M) des expressions de T devient passée.

La hiérarchie de force des théories

Ces modèles successifs, séparés par des temps infinis, forment une succession illimitée, reflétée par une une hiérarchie illimitée de théories qui les décrivent respectivement. Cette hiérarchie sera évoquée en termes d'une comparaison de force entre les théories (ce qui forme un préordre). A savoir, une théorie A est dite plus forte qu'une théorie B si (une copie de) B peut être trouvée contenue dans A ou un développement possible de A; elles sont de même force si cela vaut aussi vice-versa. En effet, les développements ne sont que des "mouvements finis" négligés par le concept de force qui vise à ne retenir que les "mouvements infinis". (Une autre définition de l'ordre de force, souvent mais peut-être pas toujours équivalente, viendra en 1.C).

De nombreuses forces seront représentées par des versions de la théorie des ensembles, nous permettant ainsi d'appeler des «univers» ces modèles successifs. Ainsi, toute théorie des ensembles visant à décrire un univers de «tous les objets mathématiques», ce n'est à chaque instant que le «tout» actuel, fait de notre passé; tandis que cette description elle-même forme autre chose au-delà de ce «tout».

Axiomes renforçants de la théorie des ensembles

Alors que notre étude se concentrera sur les théories des ensembles acceptant d'autres notions que les ensembles (comme annoncé en 1.4), la différence avec les théories des ensembles traditionnelles (dont les seuls objets sont des ensembles) peut être ignorée, car toute bonne théorie des ensembles formalisée à notre manière est de même force qu'une avec seulement des ensembles, et de même vice versa.
Nos théories des ensembles, au-delà de leur liste commune de symboles et d'axiomes de base "nécessaires" (2.1 et 2.2), différeront principalement par leur force, selon leurs choix d'axiomes renforçants optionnels (parfois accompagnés de symboles primitifs), dont le rôle sera encore commenté en 1.D et 2.C. Les principaux axiomes renforçants sont:

Les principales théories fondatrices

En introduction simplifiée, voici quelques-unes des principales théories fondatrices (toutes des théories du premier ordre, même "l'arithmétique du second ordre"), ordonnées par force croissante (tandis que des infinités d'autres forces existent également entre elles et au-delà). La partie la plus difficile de la preuve de Gödel de ses fameux théorèmes d'incomplétude était de développer TT à partir de Z1, de sorte que les résultats d'incomplétude initialement prouvés pour TT affectent également Z1. Cette difficulté peut être ignorée en se concentrant sur TT et FST, en ignorant Z1. Développer TT à partir de FST est facile (une fois que TT est formalisé), mais les développer à partir de Z1 est plus difficile. Une solution est de développer la version "ensembles seuls" de FST à partir de Z1 en définissant le prédicat BIT (en guise de ∈) et en prouvant ses propriétés de base; la difficulté de le faire peut être évitée en les acceptant comme primitifs.

1.B. Indéfinissabilité de la vérité

Poursuivant notre introduction à la vue d'ensemble des fondements des mathématiques, esquissons un aspect particulier de l'ordre temporel des interprétations: l'incapacité des théories auto-descriptives à définir (prédire) les valeurs de leurs propres énoncés. Cela confirmera le rôle de la hiérarchie des forces des théories et sera une étape clé dans la preuve de l'incomplétude de l'arithmétique (et donc de la logique du second ordre).

Objets standard et citations

Les objets dans les modèles standard d'une FOT seront eux-mêmes appelés standard, ce qui intuitivement signifie "vraiment fini". Ils peuvent en principe être mathématiquement cités: pour chaque objet x, on peut former un terme clos, ici abrégé par la notation ⌜x⌝, et qui désigne x dans le modèle standard. Ainsi, le modèle standard de l'arithmétique ℕ est composé de nombres standard, valeurs n de citations ⌜n⌝ du style 1+...+1 (les détails effectifs seront étudiés dans la partie 4).
Les références à la vérité des énoncés et à la signification des classes des FOT seront implicitement entendues comme leurs interprétations standard, sauf indication contraire.

Les modèles non standard peuvent être compris comme des extensions du modèle standard: ils contiennent aussi tous les objets standard, copies des objets du modèle standard, définis comme valeurs de leurs citations mathématiques; mais diffèrent en ayant d'autres objets au-delà, appelés objets non standard (non citables). Les nombres non standard seront également appelés pseudo-finis: vus par la théorie comme «finis» mais avec le schéma de propriétés d'être «absolument indescriptiblement grands»: supérieurs à tout nombre standard, donc en fait infinis.
Dans les expressions d'énoncés ou de classes de théories fondatrices, il n'y a généralement aucune différence à permettre des paramètres de valeur finie (= dont le type appartient à une partie FOT de la théorie) dans la mesure où ils sont plus précisément destinés à ne prendre que des valeurs standard, et peuvent donc être remplacés par leurs citations.

Dans un modèle non standard de FST, les ensembles standard sont les ensembles vraiment finis d'éléments tous standard. Mais cela ne définit pas la standardité, qu'on ne peut pas non plus définir par les citations (qui sont une infinité de méta-objets). Comme il sera clair dans la partie 4, le schéma d'axiomes rend la standardité indéfinissable par toute formule de FOT: le méta-ensemble des objets standard dans un modèle non standard n'est pas une classe, et donc (pour FST) pas un ensemble.

Théorèmes d'indéfinissabilité de la vérité

Toute théorie descriptible T plus forte que TT (= capable d'exprimer TT) peut également se décrire elles-même: les définitions des τ, L, X composant T forment le développement à partir de TT (et donc de T) de la version de 1TT décrivant T. Mais cela ne sera pleinement utilisé que pour les théorèmes d'incomplétude (1.C). D'abord, l'indéfinissabilité de la vérité utilisera TT (avec des notions générales d'expressions) mais pas X (distinction des axiomes parmi les énoncés; les τ et L habituels étant finis sont sans problème).
(Une version de 1TT avec τ, L ou X non défini, n'étant pas un développement de TT proprement dit, son fonctionnement nécessiterait d'ajouter l'utilisation de τ, L, X dans le schéma d'axiomes : d'induction pour Z1, ou de compréhension pour FST ...).

Soit S la méta-classe des énoncés de T, et S la classe définie dans 1TT et donc dans T pour jouer le rôle de S dans tout modèle M de T. Pour tout énoncé F∈S, sa citation ⌜F⌝ désigne dans M l'élément de S jouant le rôle de cet énoncé : 1TT⊢ (⌜F⌝∈S).

Soit S1 la méta-classe des formules de T avec une seule variable libre (de domaine S mais ce détail peut être ignoré), visant à définir des prédicats invariants de domaine S. Alors aucun d'eux ne peut coïncider avec la véracité des énoncés dans le même modèle:

Théorème d'indéfinissabilité de la vérité (version faible). Pour tout modèle M de T, la méta-classe {A∈S | M⊨A} des énoncés vrais dans M, diffère de toute classe invariante, dans M, d'objets "énoncés":

∀C∈S1, ∀M⊨T, ∃A∈S, M⊨ (A ⇎ C(⌜A⌝))

Théorème d'indéfinissabilité de la vérité (version forte). ∀C∈S1, ∃A∈S, T ⊢ (A ⇎ C(⌜A⌝)).

La tradition se concentre sur la démonstration de la version forte (détails en partie 5): la preuve utilisant le paradoxe du menteur fournit un A explicite, défini comme ¬C(⌜A⌝) où la citation ⌜A⌝ est obtenue par une technique d'auto-référence explicite (finitiste) mais complexe. Elle donne donc l'information "pure" d'un "inconnu connu": l'échec nécessaire de C à interpréter un A explicite "simplement" fait de ¬C appliqué à un terme clos complexe.

Mais la version faible peut être prouvée d'une autre manière, par le paradoxe de Berry (les détails impliquant des subtilités dans les fondements de l'arithmétique ont été déplacés vers la partie 4): à partir d'une définition de la vérité des énoncés, on peut définir le prédicat entre formules et nombres disant quelle formule définit quel nombre, et donc définit un nombre du style "le plus petit nombre non définissable en moins de vingt mots" qui conduirait à la contradiction.
Cette preuve est à la fois plus intuitive (évitant les difficultés d'auto-référence) et fournit une information différente: elle montre l'omniprésence de «l'inconnu inconnu» donnant un ensemble fini d'énoncés A qui sont «moins purs» en leur genre mais moins complexes en taille, parmi lesquelles une "erreur" doit exister, sans préciser où (cela dépend du nombre qui serait ainsi "défini").

La hiérarchie des formules

Les faits d'indéfinissabilité de la vérité, d'indécidabilité ou autre indétermination des formules peuvent être compris en analysant leur syntaxe, comme provenant principalement de leur utilisation de symboles liants: les formules les mieux définies sont celles sans symboles liants; puis, intuitivement, la clarté de sens d'un symbole liant donné tient à la mesure dont son domaine peut être qualifié d'ensemble. Dans les théories des ensembles, les quantificateurs ouverts (de domaine l'univers ou une classe) sont moins clairs que les quantificateurs bornés et autres symboles liants de domaine un ensemble.

Pour FST, la condition essentielle pour qu'une classe soit un ensemble est la finitude. De même en arithmétique, les quantificateurs peuvent être bornés en utilisant l'ordre: (∃x<k, ) et (∀x<k, ) abrègent respectivement (∃x, x<k ∧ ) et (∀x, x<k ⇒ ) et de même pour ≤.
Les valeurs des énoncés bornés des FOT sont indépendants du modèle car leur interprétation n'utilise que des objets standard. Tout objet standard d'un FOT a toutes les mêmes propriétés bornées (= exprimées par des formules bornées sans autre variable libre) dans tout modèle.

Versions raffinées

Les preuves des théorèmes d'indéfinissabilité de la vérité, donnant explicitement un A sur lequel chaque C diffère de la vérité, prouvent plus que leurs simples conclusions: elles précisent en quelque sorte l'étendue de cette différence. A savoir : Cette dernière équivalence s'obtient en développant certains quantificateurs FOT-bornés, donc de domaines finis ; sa preuve n'utilise que des axiomes de TT, bien que C puisse utiliser un langage plus large. Donc si C est admissible sur toute la classe des énoncés de T, est constant entre les énoncés TT-prouvablement équivalents, et opère fidèlement les connecteurs sur les instances de C, alors C diffère de la vérité sur certains C(⌜B⌝) :

∃B∈S, C(⌜B⌝) ⇎ C(⌜C(⌜B⌝)⌝)

Pour chaque cas (faible ou fort), en un certain sens, A n'a pas besoin de plus de quantificateur de chaque sorte que C. Donc, tout C borné diffère de la vérité sur certains A bornés. Dans les FOT une telle différence est assez grave, mais pas surprenante faute de candidats C bornés approchant la vérité à considérer.

Prédicats de vérité

Appelons prédicat de vérité d'une théorie T décrite par une autre théorie T', tout prédicat C (défini par T' avec de possibles paramètres) sur la classe S d'énoncés de T, de sorte que
  1. ∀A∈X, C(A) : il contient tous les axiomes de T
  2. ∀A∈S, C(A)∨C(¬A)
  3. C est cohérent.
De manière équivalente, 2. et 3. peuvent être remplacés par
  1. ∀A∈S, C(A) ⇎ C(¬A)
  2. C contient toutes les conséquences logiques des conjonctions de ses éléments.
L'existence d'un prédicat de vérité de T implique évidemment sa cohérence. Mais la réciproque est également TT-prouvable, ce qui rend ces équivalents:
Si T est cohérent alors il permet de (TT-prouvablement) TT-définir un prédicat de vérité de T ainsi:
  1. Prendre tous les énoncés dans un ordre arbitraire;
  2. Ajouter chacun aux axiomes s'il est cohérent avec les axiomes précédemment acceptés.
Une telle définition n'est pas algorithmique (la condition "si cohérent" est invérifiable en temps fini), mais n'utilise aucun autre paramètre que T et un ordre sur son langage.

Propriétés des modèles

Les propriétés (du premier ordre) d'un modèle M de T, sont les énoncés de T vrais dans M.
La classe des propriétés de tout modèle de T est un prédicat de vérité de T. Mais cela n'a pas toujours de sens à cause de l'indéfinissabilité de la vérité : TT manque de définitions générales pour les classes de propriétés des systèmes infinis avec des nombres illimités de quantificateurs. Leur signification systématique ne vient que dans des cadres strictement plus forts tels que MT, pouvant tenir comme ensembles certaines classes infinies (telles que les classes d'objets finis) servant de types (classes d'objets) dans M.

Le théorème de complétude, simplement exprimé dans des théories des ensembles avec Infini, apparaît aussi dans TT comme un schéma de théorèmes qui, pour toute définition d'une théorie cohérente, conçoit un modèle comme une classe d'objets avec des structures définies par TT. La construction simple de notre preuve en 4.7 garantit la vérité des axiomes mais ignore les autres énoncés. En suivant cette construction, tous les énoncés s'interprètent comme cas particuliers d'énoncés TT (de paramètres τ, L, X composant T, à remplacer par leurs définitions). Le prédicat de vérité ainsi obtenu sur cette classe peut ne pas être invariant TT, mais est de toute façon invariant MT du moment que T l'était (car MT peut définir la vérité sur la classe des énoncés TT).

Mais l'application du théorème de complétude à un prédicat de vérité donné (qui peut être défini par TT), prouve dans TT l'existence d'un modèle dont les propriétés lui sont conformes, bien que ses notions interprétées ne soient pas des ensembles. Cela présente en 2 étapes comment construire un modèle avec des propriétés invariantes TT, mais le même objectif est également atteint par la construction unique mais plus difficile de la preuve traditionnelle (par Henkin) du théorème de complétude.

1.C. Introduction aux théorèmes d'incomplétude

Classes existentielles

Qualifions une formule d'existentielle si elle s'écrit ∃x, A(x), avec un ∃ ouvert comme racine (ou plusieurs, qui peuvent être ré-exprimés comme un seul) suivi d'une formule bornée A. Dans cette section, cela sera entendu au sens de FOT uniquement. Les énoncés existentiels expriment essentiellement les conditions d'arrêt des algorithmes opérés par des "ordinateurs" abstraits aux ressources illimitées. De même, une classe existentielle d'un FOT, à savoir définie par une formule existentielle ∃y, A(y,x), peut de manière équivalente être qualifiée d'algorithmiquement définie, comme ensemble de toutes les données de sorties fournies en cours de route par un algorithme sans fin; elle définit la vérité sur les énoncés existentiels obtenus en remplaçant x par toute citation.

Prédicats de prouvabilité

Les concepts de provabilité sont liés aux classes existentielles comme suit. Les classes existentielles de "théorèmes" habituelles parmi les énoncés du premier ordre de langage donné, sont formées en 2 étapes:
  1. Donner une théorie du premier ordre avec une classe existentielle d'axiomes (celles habituelles, dont toutes les théories de notre liste, ont même des définitions bornées);
  2. Lui appliquer le concept de preuve de la logique de premier ordre.
La classe de théorèmes qui en résulte est indépendante de la définition formelle choisie pour un concept correct et complet de preuve en logique du premier ordre, en ce sens que deux d'entre elles donnant des formules V, V', exprimant la vérification de preuve dans la même théorie (définie par les symboles τ, L, X), elles donnent les mêmes théorèmes:

FOT (+ symboles τ, L, X avec axiomes) ⊢ ∀s, (∃p, V(p,s)) ⇔ (∃p, V'(p,s))

Comme la première étape définit τ, L, X dans FOT, elle simplifie ce qui précède en FOT ⊢ ...

Inversement, si C est une classe existentielle de "théorèmes" parmi les énoncés du premier ordre d'une théorie, et contient les conséquences logiques du premier ordre de toute conjonction de ses éléments (intuitivement, le cadre de démonstration contient la puissance de la logique du premier ordre), alors C est la classe des énoncés T-prouvables par la logique du premier ordre, pour une théorie du premier ordre algorithmiquement définie T: au moins trivialement, la théorie prenant C comme classe d'axiomes.

Une théorie T plus forte que FOT sera qualifiée de FOT-correcte si, dans la classe des énoncés FOT, la T-prouvabilité implique la vérité (dans le modèle standard de FOT).

La diversité des modèles non standard

Au-delà du simple fait d'existence des modèles, les diverses façons de les construire et leurs cas d'utilisation (théories) fourniront une diversité de modèles, y compris des modèles non standard de théories fondatrices, plus ou moins similaires aux modèles standard.

Même avec des propriétés de premier ordre identiques (une condition qu'on peut adopter en prenant comme «axiomes» tous les énoncés vrais d'un modèle donné, bien que ce ne soit pas TT-invariant pour les modèles standard de théories plus fortes que TT), les modèles peuvent différer par des propriétés de niveau méta: cela sera vu pour l'arithmétique en 4.9, et pour toute théorie avec un modèle infini par le théorème de Löwenheim-Skolem.
Mais l'indéfinissabilité de la vérité implique que certains modèles construits diffèrent également par des propriétés du premier ordre à cause de leur invariance. Ceci vaut même pour des théories fondatrices "presque complètes" (pouvant notamment approcher une théorie complète du second ordre par élimination universelle du second ordre).

Toutes les théories fondatrices étant TT-invariantes, ont des modèles aux propriétés FOT-invariantes, donc déjà non standard pour leurs propriétés FOT.
Toute théorie T invariante MT, cohérente et plus forte que MT, a des modèles MT-invariants et MT-interprétables (en particulier, tout modèle FOT-invariant est TT-interprétable), donc une classe de propriétés MT non standard (une fois clarifié un concept de "modèle standard de MT" ...). Si de plus T est FOT-correcte, l'ajout de tous les énoncés vrais FOT aux axiomes donne encore une théorie cohérente et invariante MT, donnant des modèles de T avec la classe standard de propriétés FOT mais d'autres propriétés MT non standard (et très probablement un modèle de FOT non standard).

Premier théorème d'incomplétude

Soit C une classe d'énoncés FOT "T-prouvables" pour une théorie algorithmiquement définie T capable de les exprimer (C est une classe existentielle d'énoncés FOT contenant les conséquences logiques du premier ordre de toute conjonction de ses éléments). Par indéfinissabilité de la vérité faible, C étant FOT-invariant doit différer de la vérité : C(⌜A⌝) ⇎ A pour certains A.
Si T est FOT-correct (C(⌜A⌝) ⇒ A pour tout A), alors pour chaque A sur lequel C diffère de la vérité, A est T-indémontrable mais vrai, et donc T-indécidable. Ainsi T est incomplet (laissant indécidables certains énoncés FOT). D'où l'incomplétude de la logique du second ordre (1.11). Cela approche, mais ne donne pas, le célèbre

Premier théorème d'incomplétude. Toute théorie définie par algorithme cohérente et plus forte que FOT est incomplète.

L'écart peut être négligé, car c'est un défaut pire pour une théorie d'être FOT-incorrecte que d'être incomplète. Mais il peut encore être réduit en utilisant notre version raffinée de l'indéfinissabilité faible comme suit.
Supposons T plus fort que FOT (C contient tous les axiomes de FOT, et donc ses théorèmes). Alors pour tout A existentiel, et donc pour A de la forme C(B) pour tout B,

A ⇒ (A est FOT-prouvable) ⇒ C(⌜A⌝)

Si T est cohérent et décide tous les C(A), alors C opère fidèlement les connecteurs sur les instances de C (en déduisant les résultats des valeurs prouvées de C, même si elles sont incorrectes). Donc: (La littérature rapporte des possibilités de prouver les deux théorèmes d'incomplétude par le paradoxe de Berry, mais cela semble très compliqué, au-delà de la portée de cette introduction.)

Second théorème d'incomplétude

Le second théorème d'incomplétude (dont la preuve utilise la version forte de l'indéfinissabilité de la vérité) dit que C(A) est T-iirréfutable pour tous les énoncés A si seulement T est cohérent :

¬C(⌜0⌝) ⇒ ∀A∈S, ¬C(⌜¬C⌝:A)

où les deux points ( : ) signifient la substitution entre les expressions décrites de sorte que (⌜B⌝:⌜a⌝) = ⌜B(a)⌝. Ceci se résume au cas A=⌜0⌝, à savoir C(⌜¬C(⌜0⌝)⌝) ⇒ C(⌜0⌝) autrement dit la cohérence de T, si elle est vraie, est T-indémontrable.
Reformulant ceci par complétude, si T n'a pas de contradiction standard, alors elle a un modèle contenant une contradiction non standard (et donc ne contenant pas de modèle vérifiable).

Aussi de manière équivalente, T ne peut prouver l'existence d'aucun prédicat de vérité sur une notion qu'elle décrit comme l'ensemble de ses propres énoncés. Ceci est en quelque sorte expliqué, bien que pas directement impliqué, par la faible indéfinissabilité de la vérité, qui empêche d'utiliser le modèle actuel comme exemple, car la vérité sur tous les énoncés standard ne peut pas y être T-définie comme un prédicat invariant (même pas spéculativement, c'est-à-dire valable uniquement dans certains modèles).

Le temps des démonstrations

Comme la T-prouvabilité de tout énoncé A ne peut pas être T-réfutée, quelle que soit la quantité de recherche vaine de T-preuves, cela signifie que T continue de "voir une chance" que A soit T-prouvable par des preuves plus longues. Une théorie T' strictement plus forte que T peut réfuter la T-prouvabilité de certains A (notamment en trouvant une T-réfutation de A) mais reste indécise pour d'autres (comme A = l'incohérence de T').
Toute théorie fondatrice FOT-correcte (prise comme critère de connaissance) laissera toujours certains énoncés existentiels pratiquement indécidables, qu'ils soient réellement vrais ou faux, la recherche de preuves ou de réfutations semblant vaine dans les limites données de ressources de calcul disponibles: Comme autre aspect du même fait, les prédicats de prouvabilité sont inexprimables par les formules bornées (en raison de l'indéfinissabilité de la vérité, car ils sont équivalents à la vérité dans la classe des énoncés bornés).
Intuitivement, interpréter la vérité sur des énoncés existentiels (ou tout prédicat de T-provabilité), nécessite une vue réaliste : une utilisation de l'infini actuel de ℕ précisément entendu comme son interprétation standard (qui ne peut pas être complètement axiomatisée).

Par une sorte de paradoxe, alors que le théorème de complétude est prouvé en construisant (à l'aide de l'infini actuel) un contre-exemple (modèle) à partir du fait de l'absence de preuve, il n'y a pas de "construction inverse" qui, partant du fait sur l'infini qu'aucun système ne peut exister avec des propriétés données, produirait un témoin fini qui en est la preuve (qui doit néanmoins exister).
Au lieu de cela, l'analyse de cette construction révèle que la taille (complexité) d'une preuve reflète en gros le nombre d'éléments bien choisis qui doivent être décrits dans une tentative de construction d'un contre-exemple, pour découvrir l'échec nécessaire d'une telle construction; la formalisation choisie de la théorie de la démonstration ne peut affecter la taille des preuves que dans des proportions plus modérées (descriptibles).

1.D. La théorie des ensembles comme cadre unifié

Définisseurs de structure dans diverses théories

Appelons définisseur de structure tout symbole liant B qui enregistre fidèlement la structure unaire (relation, resp. fonction) définie par toute expression entrée (formule, resp. terme) A sur un domaine E (type, classe ou ensemble ici fixé), à savoir que son résultat S = (Bx, A(x)) peut restaurer cette structure par un évaluateur V (symbole ou expression): ∀E x, V(S, x) = A(x).
Admettant l'utilisation de la négation et la possibilité d'interpréter des booléens par des objets (dans un ensemble à au moins deux objets, comme cela arrive souvent), le paradoxe de Russell montre que l'ajout des deux exigences suivantes à un définisseur de structure dans une théorie conduirait à une contradiction:
  1. Tous ces S appartiennent à E
  2. V peut apparaître dans l'expression A et utiliser x n'importe comment dans ses arguments. Donc V(x, x) est autorisé, ce qui est normal comme 1. garantit l'admissibilité de tout V(S, S).
Enumérons les options restantes. La théorie des ensembles rejette 1. mais conserve 2. Mais puisque 1. est rejeté, conserver 2. peut être un problème ou non suivant les cas plus précis.

Dans la construction (1.5) d'un type K de structures défini par une formule A, un symbole liant de domaine K abrège une utilisation successive de symboles liants sur tous les paramètres de A. Ici, A et le modèle l’interprétant viennent d'abord, puis l'ensemble K de structures avec son évaluateur V sont créés en dehors: A n'a pas de sous-terme de type K, donc n'utilise pas V.

La notion de structure dans 1MT (théorie du modèle en logique du premier ordre), présente cette similitude avec la notion d'ensemble en théorie des ensembles: dans 1MT, la classe de toutes les structures de chaque type de symbole fixé (au-delà des constantes) n'est généralement pas un ensemble, appelant "ensembles" de tels ensembles K (de celles définies par une expression fixe avec des paramètres variables), et leurs sous-ensembles.
Cette similitude peut se formaliser en regroupant tous ces K du même type de symbole (construits pour toutes les expressions possibles A) en un seul type U, avec le même évaluateur V (ces A peuvent utiliser V mais pas le domaine U). Cette fusion d'une infinité d'ensembles en un ne fait que réécrire ce qu'on pouvait déjà faire sans cela, tant que les variables de type U ne sont liées que sur un de ces "ensembles" K (ou de façon équivalente un ensemble couvert par un nombre fini d'entre eux).

En théorie des ensembles, les domaines des symboles liants sont les ensembles. Ainsi, au-delà de l'avantage simplificateur de supprimer les types, la théorie des ensembles gagnera de la puissance par ses axiomes renforçants qui reviennent à accepter plus de classes comme ensembles.

D'autres théories, que nous ignorerons dans la suite de ce travail, suivent des options plus audacieuses:

Le cadre unifié des théories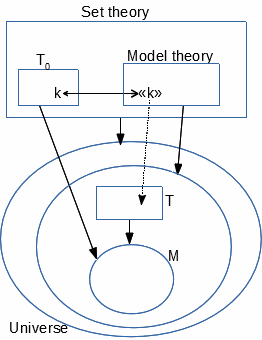

Comme l'arithmétique (et autres FOT), formaliser TT ou tout 1TT en tant que théorie complète, requiert un axiome de second ordre pour exclure les modèles non-standard avec des «expressions» et «preuves» pseudo-finies. Or, le meilleur environnement pour de telles théories du second ordre (donnant une apparence de détermination unique, non réelle), et aussi pour MT ou 1MT, est l'insertion dans une version suffisamment forte de la théorie des ensembles (qui peut définir la finitude: voir 4.6). Cette insertion transformant les composants en variables libres qui ensemble désignent le modèle, leur variabilité élimine la principale différence entre TT et 1TT, et entre MT et 1MT (une autre différence est que MT peut décrire des théories incohérentes). Ce développement de la théorie des modèles à partir d'une version suffisamment forte de la théorie des ensembles viendra dans les parties 3 et 4, complétant le grand tour des fondements des mathématiques après la formalisation de la théorie des ensembles (principalement par les parties 1 et 2).

Pour une théorie T ainsi décrite, soit T0 la théorie externe, également insérée en théorie des ensembles, qui ressemble à une copie de T comme tout composant k de T0 a une copie comme objet servant de composant de T. Dans une formalisation appropriée, T0 peut être défini à partir de T comme formé des k tel que Univers⊨ ⌜k⌝∈T, ce qui signifie que la valeur de la citation ⌜k⌝ interprétée dans l'univers, appartient à T.
Mais il n'y a pas de définition inverse générale, de T à partir d'un T0 avec une infinité de composants, car un objet ne peut pas être défini à partir d'une infinité donnée de méta-objets. Toute liste infinie de composants de T0 doit répondre à une définition, pour obtenir l'image idéalisée T de T0 en interprétant cette définition dans l'univers. (La formule de définition doit être bornée pour que T0 corresponde à la définition ci-dessus par ce T).

Ceci forme un cadre commode pour décrire les théories et leurs modèles, unifiant les deux cadres précédents (ensembliste et modèle-théorique): tous les travaux de T0 (expressions, preuves et autres développements), ont des copies comme objets (en interprétant leurs citations) décrits formellement par le développement modèle-théorique de la théorie des ensembles comme travaux de la théorie T. Dans le même univers, tout système M décrit comme modèle de T est indirectement aussi un modèle (ensembliste) de T0.
Mais en tant que théorie du premier ordre, la théorie des ensembles ne peut pas exclure les univers non standard, dont l'interprétation des FOT est non standard (avec des objets pseudo-finis). Dedans, les discordances suivantes entre T0 et T peuvent se produire: Ainsi comprises, les conditions de validité de ce cadre unifié sont habituellement acceptées comme des hypothèses légitimes, en se concentrant sur des théories bien décrites, interprétées dans des univers standard dont l'existence est admise pour des raisons philosophiques.

La théorie des ensembles comme cadre unifié d'elle-même

L'application de ce cadre unifié au choix d'une théorie des ensembles dans le rôle de T0 (décrivant M et idéalisée comme objet T) élargit les outils d'interprétation de la théorie des ensembles dans elle-même (1.7). Comme T0 coexiste au même niveau avec la théorie des ensembles servant de cadre, on peut les prendre comme copies exactes l'une de l'autre (sans problème de standardité), ce qui revient à prendre la même théorie des ensembles avec deux interprétations: M appelé "univers", et l'interprétation cadre appelée "méta-univers ".
Mais le second théorème d'incomplétude les fait différer comme suit. L'énoncé d'existence d'un univers d'une théorie des ensembles donnée T (et donc aussi l'énoncé plus fort de l'existence d'un univers standard), exprimé comme énoncé ensembliste interprété dans le méta-univers, ne peut pas être un théorème de T. Cela montre la nécessaire diversité des forces entre les théories axiomatiques des ensembles utiles, qui sera commentée plus en détail en 2.C.

Le paradoxe de Zénon

Achille poursuit une tortue ; à chaque fois qu'il parcourt la distance qui l'en sépare, celle-ci prend une nouvelle longueur d'avance.
Vu d'une hauteur, un véhicule parti sur une route horizontale se rapproche sans cesse de l'horizon.
Les particules sont envoyées dans les accélérateurs de plus en plus près de la vitesse de la lumière.
Peuvent-ils atteindre leur but ?
Chaque exemple peut être vu de 2 manières: Dans chaque exemple, une mesure physique du «coût» pour approcher et éventuellement atteindre l'extrémité visée, décide quelle est sa seule «vraie» lecture, suivant que ce coût serait fini ou infini (ce qui peut différer des suppositions d'un observateur naïf).
Mais le monde des mathématiques, libre de toute mesure de coût physique et où les objets ne font que jouer des rôles conventionnels, peut accepter les 2 points de vue.

Chaque théorie générique pouvant utiliser des symboles liants sur des types, elle considère les types comme des ensembles et «atteint la fin» de son modèle qu'elle voit comme un tout «fermé». Mais tout cadre qui l'englobe (théorie du modèle ou théorie des ensembles) échappe à cette totalité. Or, la théorie des ensembles a de multiples modèles, d'un univers à un méta-univers (contenant plus d'ensembles: les méta-ensembles, et de nouvelles fonctions entre eux) et ainsi de suite (un méta-méta-univers ...). Pour refléter les possibilités illimitées d'échapper à tout univers donné, on a besoin d'une théorie «ouverte» intégrant chaque univers comme partie (passée) d'un univers ultérieur, formant une succession illimitée de réalités croissantes, sans perspective sur son éventuelle totalité. Ce rôle de théorie ouverte sera joué par la théorie des ensembles elle-même, par la manière dont ses expressions ne lient les variables que sur des ensembles.

Other languages: EN : 1. First foundations of mathematics